Biết rằng khối tứ diện đều cạnh bằng k thì có thể tích bằng 2 k 3 12 . Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a 2 . Tính theo a thể tích khối tứ diện A C B ' D ' .
A. 2 2 a 3 3
B. 2 a 3 6
C. 2 a 3 2
D. a 3 3
Cho khối tứ diện đều \(ABCD\) cạnh \(a\). Chứng minh rằng thể tích của khối tứ diện đó bằng \(\frac{{{a^3}\sqrt 2 }}{{12}}\).
.png)
Gọi \(M\) là trung điểm của \(BC\), \(O\) là trọng tâm tam giác \(ABC\).
\( \Rightarrow SO \bot \left( {ABC} \right)\)
Tam giác \(ABC\) đều
\( \Rightarrow AM = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2} \Rightarrow AO = \frac{2}{3}AM = \frac{{a\sqrt 3 }}{3}\)
Tam giác \(SAO\) vuông tại \(O \Rightarrow SO = \sqrt {S{A^2} - A{O^2}} = \frac{{a\sqrt 6 }}{3}\)
\(\begin{array}{l}{S_{\Delta ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{4}\\{V_{S.ABC}} = \frac{1}{3}{S_{\Delta ABC}}.SO = \frac{{{a^3}\sqrt 2 }}{{12}}\end{array}\)
Cho khối tứ diện đều có tất cả các cạnh bằng 2a. Thể tích khối tứ diện đã cho bằng
A. a 3 2 6
B. a 3 2 12
C. a 3 2 3
D. 2 a 3 2 3
Cho khối tứ diện đều có tất cả các cạnh bằng 2a. Thể tích khối tứ diện đã cho bằng:
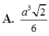
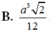
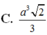
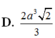
Cho khối chóp đều S.ABC, đáy có cạnh bằng a, cạnh bên bằng b. Tính thể tích của khối chóp đó. Từ đó suy ra thể tích của khối tứ diện đều có cạnh bằng a.
Kẻ SG vuông góc (ABC)
S.ABC là khối chóp đều
=>ΔABC đều
=>G là trọng tâm, là trực tâm của ΔABC
Gọi giao của AG với BC là D
=>D là trung điểm của BC
ΔABC đều có AD là trung tuyến
nên \(AD=\dfrac{a\sqrt{3}}{2}\)
=>\(AG=\dfrac{a\sqrt{3}}{2}\cdot\dfrac{2}{3}=\dfrac{a\sqrt{3}}{3}\)
ΔSAG vuông tại G nên \(SG=\sqrt{SA^2-AG^2}=\sqrt{b^2-\dfrac{1}{3}a^2}\)
\(V_{S.ABC}=\dfrac{1}{3}\cdot S_{ABC}\cdot SG=\dfrac{1}{3}\cdot\sqrt{b^2-\dfrac{1}{3}a^2}\cdot\dfrac{a^2\sqrt{3}}{4}\)
\(=\dfrac{a^2\sqrt{3}}{12}\cdot\sqrt{\dfrac{3b^2-a^2}{3}}\)
Thể tích khối tứ diện đều có cạnh bằng a là:
\(V=\dfrac{a^2\sqrt{3}}{12}\cdot\sqrt{a^2-\dfrac{a^2}{3}}=\dfrac{a^3\sqrt{2}}{12}\)
Cho hình chóp tứ giác đều có cạnh đáy bằng a và biết diện tích xung quanh gấp đôi diện tích đáy. Thể tích của khối chóp đã cho bằng
A. a 3 3 2
B. a 3 3 3
C. a 3 3 6
D. a 3 3 12
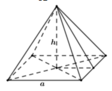
Gọi chiều cao của hình chớp là h. Khi đó ta tính được diện tích xung quanh của hình chóp là 
Theo yêu cầu bài toán 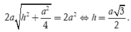
Thể tích khối chóp là: ![]()
Chọn C.
Cho hình chóp tứ giác đều S.ABCD, đuờng cao SO. Biết rằng trong các thiết diện của hình chóp cắt bởi các mặt phẳng chứa SO, thiết diện có diện tích lớn nhất là tam giác đều cạnh bằng a, tính thể tích khối chóp đã cho
A. a 3 2 6
B. a 3 3 12
C. a 3 3 4
D. a 3 3 6
Cho tứ diện ABCD có ABCD và D A ⊥ A B C ; DA = 1 là tam giác đều cạnh bằng 1. Trên ba cạnh DA, DB, DC lấy 3 điểm M, N, P mà D M D A = 1 2 ; D N D B = 1 3 ; D P D C = 3 4 Tính thể tích khối tứ diện MNPD
A. V = 3 12
B. V = 2 12
C. V = 3 96
D. V = 2 96
Ta có
V D M N P V D A B C = D M D A . D N D B . D P D C = 1 2 . 1 2 . 3 4 = 1 8
Do đó 1 8 . 3 12 = 3 96
Đáp án C
Thể tích c m 3 của khối tứ diện đều có cạnh bằng 2/3 cm là:
A. 3 2 81
B. 2 2 81
C. 2 3 81
D. 2 81
Đáp án B
Công thức tính nhanh thể tích tứ diện đều cạnh a = 2 3 là: a 3 2 12 = 2 2 81
Cho tứ diện đều ABCD có cạnh bằng a. Thể tích của khối cầu tiếp xúc với tất cả các cạnh của tứ diện ABCD bằng
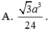
![]()
![]()
![]()