Cho tập A = x ∈ ℤ / - 1 ≤ x ≤ 5 Số tập con gồm 3 phần tử của A là
A. C 7 3
B. C 6 3
C. C 8 3
D. C 5 3
Những câu hỏi liên quan
Cho tập hợp
A
x
∈
ℤ
/
-
1
≤
x
≤
5
. Số tập con gồm 3 phần tử của A là A.
A
7
3...
Đọc tiếp
Cho tập hợp A = x ∈ ℤ / - 1 ≤ x ≤ 5 . Số tập con gồm 3 phần tử của A là
A. A 7 3
B. A 7 4
C. C 7 4
D. C 7 5
Chọn C
Lời giải.
Vì - 1 ≤ x ≤ 5 và x ∈ ℤ nên A = - 1 ; 0 ; 1 ; 2 ; 3 ; 4 ; 5 do đó số phần tử của A là 7.
Mỗi tập con của A gồm 3 phần tử là một tổ hợp chập 3 của 7 phần tử.
Vậy số tập con gồm 3 phần tử của A là C 7 3 = C 7 4
Đúng 0
Bình luận (0)
Cho tập
A
x
∈
ℤ
,
-
1
≤
x
≤
5
Số tập con gồm 3 phần tử của A là A.
C
7
3
B.
C
6
3...
Đọc tiếp
Cho tập A x ∈ ℤ , - 1 ≤ x ≤ 5 Số tập con gồm 3 phần tử của A là
A. C 7 3
B. C 6 3
C. C 8 3
D. C 5 3
Cho tập hợp
A
x
∈
ℤ
|
2
+
5
x
+
4
0
Khi đó: A. A -1 B. A -4;-1 C. A {-1} D. A {-4;-1}
Đọc tiếp
Cho tập hợp A = x ∈ ℤ | 2 + 5 x + 4 = 0 Khi đó:
A. A = -1
B. A = -4;-1
C. A = {-1}
D. A = {-4;-1}
Cho các tập hợp
A
{
2
m
−
3
|
m
∈
ℤ
}
,
B
{
5
n
|
n
∈
ℤ
}
. Khi đó
A
∩
B
là: A.
{
5
(
2
k
−
1
)
|
k
∈
ℤ
}
B.
{10k
|
k
∈
ℤ
}
C.
{3...
Đọc tiếp
Cho các tập hợp A = { 2 m − 3 | m ∈ ℤ } , B = { 5 n | n ∈ ℤ } . Khi đó A ∩ B là:
A. { 5 ( 2 k − 1 ) | k ∈ ℤ }
B. {10k | k ∈ ℤ }
C. {3 ( 2 k − 1 ) | k ∈ ℤ }
D. {7k-3 | k ∈ ℤ }
Cho tập hợp
A
x
∈
ℤ
:
2
x
x
2
+
1
≥
1
, B là tập hợp các giá trị nguyên của tham số b để phương trình x2 - 2bx + 4 0 vô ng...
Đọc tiếp
Cho tập hợp A = x ∈ ℤ : 2 x x 2 + 1 ≥ 1 , B là tập hợp các giá trị nguyên của tham số b để phương trình x2 - 2bx + 4 = 0 vô nghiệm. Khẳng định nào sau đây đúng?
A. A = ∅.
B. A ⊂ B.
C. B ⊂ A.
D. B = ∅.
Đáp án: B
2 x x 2 + 1 ≥ 1 ⇔ 2 x - x 2 - 1 x 2 + 1 ≥ 0 ⇔ 2 x - x 2 - 1 ≥ 0 ⇔ - ( x - 1 ) 2 ≥ 0 ⇔ x = 1 ⇒ A = { 1 } .
∆ ' = b 2 - 4 . Để phương trình vô nghiệm thì
∆ ' < 0 ⇔ b 2 - 4 < 0 ⇔ b 2 < 4 ⇔ - 2 < b < 2 ⇒ B = { - 1 ; 0 ; 1 } . ⇒ A ⊂ B .
Đúng 0
Bình luận (0)
Cho hai tập hợp
M
{
8
k
+
5
|
k
∈
ℤ
}
,
N
{
4
l
+
1
|
l
∈
ℤ
}
.Khẳng định nào sau đây là đúng? A.
M
⊂
N
B.
N
⊂
M
C.
M
N
D.
M
∅
,
N
∅
Đọc tiếp
Cho hai tập hợp M = { 8 k + 5 | k ∈ ℤ } , N = { 4 l + 1 | l ∈ ℤ } .
Khẳng định nào sau đây là đúng?
A. M ⊂ N
B. N ⊂ M
C. M = N
D. M = ∅ , N = ∅
Cho hàm số
f
x
a
x
4
+
2
b
x
3
-
3
c
x
2
-
4
d
x
+
5
h
a
,
b
,
c
,
d
,...
Đọc tiếp
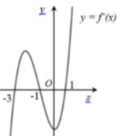
Cho hàm số f x = a x 4 + 2 b x 3 - 3 c x 2 - 4 d x + 5 h a , b , c , d , h ∈ ℤ . Hàm số y=f'(x) có đồ thị như hình vẽ bên. Tập nghiệm thực của phương trình f(x)=5h có số phần tử bằng:
A. 3
B. 4
C. 2
D. 1
Tập nghiệm của phương trình
-
9
sin
x
+
6
cos
x
-
3
sin
2
x
+
cos
2
x
-
10
là:
x
aπ
b
+
k
2
π
k
∈
ℤ
tính giá trị của
a
2
-
b
: (b...
Đọc tiếp
Tập nghiệm của phương trình - 9 sin x + 6 cos x - 3 sin 2 x + cos 2 x = - 10 là: x = aπ b + k 2 π k ∈ ℤ tính giá trị của a 2 - b : (biết a, b tối giản)
A. 3
B. - 2
C.4
D. - 1
cho hỏi ℤ là tập các số nguyên phải không?