Số đỉnh của khối bát diện đều là:
A. 6.
B. 7.
C. 8.
D. 9.
Số đỉnh của một hình bát diện đều là:
A. Sáu B. Tám
C. Mười D. Mười hai.
Chọn A.
Làm tương tự bài 1.40: 2c = 3 x 8 = 4đ, suy ra đ = 6.
Số đỉnh của khối bát diện đều là:
A. 6
A. 6
C. 8
C. 8
Số đỉnh của khối bát diện đều là:
A. 6
B. 7
C. 8
D. 9
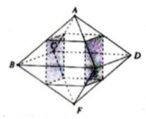
Cho hình bát diện đều ABCDEF cạnh a. Tính theo a thể tích V của khối đa diện có các đỉnh là trung điểm của các cạnh xuất phát từ đỉnh A và F của hình bát diện (xem hình vẽ)
A. V = a 3 2 .
B. V = a 3 2 4 .
C. V = a 3 2 2 .
D. V = a 3 2 8 .
Phương pháp:
Khối đa diện có các đỉnh là trung điểm của các cạnh xuất phát từ đỉnh A và F của hình bát diện đều ABCDEF (như hình vẽ) là hình hộp chữ nhật.
Cách giải:
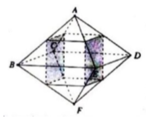
Khối đa diện có các đỉnh là trung điểm của các cạnh xuất phát từ đỉnh A và F của hình bát diện đều ABCDEF là hình hộp chữ nhật có đáy là hình vuông cạnh a 2 ;

Đếm số đỉnh, số cạnh của khối bát diện đều.
Tính thể tích của khối lập phương có các đỉnh là trọng tâm các mặt của khối bát diện đều cạnh a
A. V = 8 a 3 27
B. V = a 3 27
C. V = 16 a 3 2 27
D. V = 2 a 3 2 27
Đáp án D
Khối lập phương có các đỉnh lần lượt là trọng tâm các mặt của khối bát diện đều cạnh a có độ dài cạnh bằng x = 2 3 . a 2 2 = a 2 3 . Vậy thể tích cần tính là V = x 3 = 2 a 3 3 = 8 a 3 27
Tính thể tích của khối lập phương có các đỉnh là trọng tâm các mặt của khối bát diện đều cạnh a
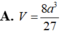
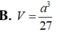
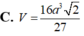
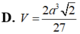
Thể tích V của khối lập phương có các đỉnh là trọng tâm các mặt của một khối bát diện đều cạnh a là
A. V = 8 a 3 27
B. V = a 3 27
C. V = 16 a 3 2 27
D. V = 2 a 3 2 27
Chọn D
Tính độ dài một cạnh của hình lập phương theo a bằng cách sử dụng định lý Ta-lét