Cho hình chóp đều S.ABCD có AB2a, SA
a
5
. Góc giữa hai mặt phẳng (SAB) và (ABCD) bằng
Đọc tiếp
Cho hình chóp đều S.ABCD có AB=2a, SA= a 5 . Góc giữa hai mặt phẳng (SAB) và (ABCD) bằng
Những câu hỏi liên quan
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có cạnh
A
B
a
,
B
C
2
a
.
Hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy (ABCD) cạnh
S
A
a
15
. Thể tích của khối chóp S.ABCD bằng A.
2
a
3
15
B....
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có cạnh A B = a , B C = 2 a . Hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy (ABCD) cạnh S A = a 15 . Thể tích của khối chóp S.ABCD bằng
A. 2 a 3 15
B. a 3 15 3
C. 2 a 3 15 3
D. 2 a 3 15 6
Cho hình chóp
S
.
A
B
C
D
có đáy
A
B
C
D
là hình thang vuông tại A và D,
S
A
B
là tam giác đều cạnh
2
a
và mặt phẳng
S
A
B
vuông góc với mặt phẳng
A
B
C
D
. Tính...
Đọc tiếp
Cho hình chóp S . A B C D có đáy A B C D là hình thang vuông tại A và D, S A B là tam giác đều cạnh 2 a và mặt phẳng S A B vuông góc với mặt phẳng A B C D . Tính cosin của góc giữa hai mặt phẳng S A B và S B C
A. 2 7
B. 2 6
C. 3 7
D. 5 7
Đáp án là A
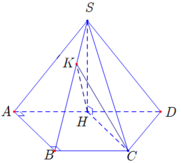
Gọi H là trung điểm của A B . Gọi K là hình chiếu vuông góc của H lên S B .
Khi đó, C K H ^ là góc giữa hai mp
Ta có: S H = 2 a 3 2 = a 3 ; S B = 2 a ; H B = a ⇒ H K = a 3 2 ; C K = a 7 2 .
Vậy cos C K H ^ = 3 7
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, ADDCa. Biết SAB là tam giác đều cạnh 2a và mặt phẳng (SAB) vuông góc với mặt phẳng (ABCD). Tính cosin của góc giữa hai mặt phẳng (SAB) và (SBC). A.
2
7
B.
2
6
C.
3
7
D.
5
7
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AD=DC=a. Biết SAB là tam giác đều cạnh 2a và mặt phẳng (SAB) vuông góc với mặt phẳng (ABCD). Tính cosin của góc giữa hai mặt phẳng (SAB) và (SBC).
A. 2 7
B. 2 6
C. 3 7
D. 5 7
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với đáy (ABCD) và SA 2a. Tính cosin của góc giữa đường thẳng SB và mặt phẳng (SAD) A.
5
5
B.
2
5
5
C.
1
2
D. 1
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với đáy (ABCD) và SA = 2a. Tính cosin của góc giữa đường thẳng SB và mặt phẳng (SAD)
A. 5 5
B. 2 5 5
C. 1 2
D. 1
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với đáy (ABCD) và SA 2a. Tính cosin của góc giữa đường thẳng SB và mặt phẳng (SAD)? A.
5
5
B.
2
5
5
C.
1
2
D. 1
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với đáy (ABCD) và SA = 2a. Tính cosin của góc giữa đường thẳng SB và mặt phẳng (SAD)?
A. 5 5
B. 2 5 5
C. 1 2
D. 1
Đáp án B
Vì ABCD là hình vuông ⇒ A B ⊥ A D 1
Ta có S A B ⊥ A B C D S A C ⊥ A B C D ⇒ S A ⊥ A B C D ⇒ S A ⊥ A B 2
Từ (1), (2) suy ra A B ⊥ S A D ⇒ S B ; S A D ^ = S B ; S A ^ = B S A ^
Tam giác SAB vuông tại A, có cos B S A ^ = S A S B = S A S A 2 + A B 2 = 2 5 5 .
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với đáy (ABCD) và SA 2a. Tính cosin của góc giữa đường thẳng SB và mặt phẳng (SAD) . A.
5
5
B.
2
5
5
C.
1
2
D .1
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với đáy (ABCD) và SA = 2a. Tính cosin của góc giữa đường thẳng SB và mặt phẳng (SAD) .
A. 5 5
B. 2 5 5
C. 1 2
D .1
Chọn B.
Phương pháp: Sử dụng định nghĩa góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, cạnh bên SAa
5
, mặt bên SAB là tam giác cân đỉnh S và thuộc mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách giữa hai đường thẳng AD và SC bằng:
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, cạnh bên SA=a 5 , mặt bên SAB là tam giác cân đỉnh S và thuộc mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách giữa hai đường thẳng AD và SC bằng:
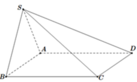
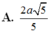
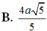
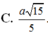
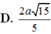
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với đáy và SA = 2a. Tính cosin góc giữa đường thẳng SB và mặt phẳng (SAD)
A. 5 5
B. 2 5 5
C. 1 2
D. 1
Cho hình chóp S.ABCD có đáy ABCD là nửa lục giác đều nội tiếp đường tròn đường kính
A
B
2
a
,
S
A
a
3
và vuông góc với mặt phẳng ABCD. Cosin của góc giữa hai mặt phẳng
S
A
D
và
S
B
C
bằng A.
2...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là nửa lục giác đều nội tiếp đường tròn đường kính A B = 2 a , S A = a 3 và vuông góc với mặt phẳng ABCD. Cosin của góc giữa hai mặt phẳng S A D và S B C bằng
A. 2 2
B. 2 3
C. 2 4
D. 2 5
