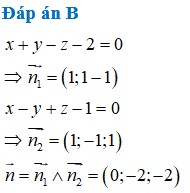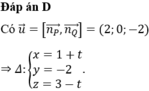Cho mặt phẳng P : x + y - z + 1 = 0 và hai điểm A 2 ; 2 ; 2 , B 4 ; 4 ; 0 .Gọi (S) là mặt cầu đi qua hai điểm A, B sao cho ∀ M ∈ ( S ) ⇒ d ( M ; ( P ) ) ≥ d ( A , ( P ) ) d ( M ; ( P ) ) ≤ d ( B , ( P ) ) .Khi đó phương trình (S) là
A. x - 3 2 + y - 3 2 + z - 1 2 = 3
B. x - 1 2 + y - 1 2 + z - 3 2 = 3
C. x - 1 2 + y - 1 2 + z - 3 2 = 9
D. x - 3 2 + y - 3 2 + z - 1 2 = 9