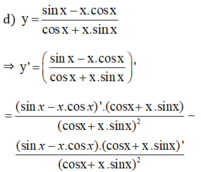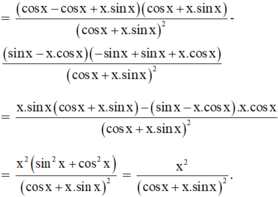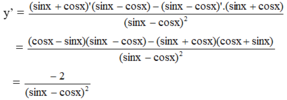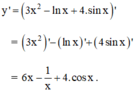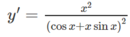Tính đạo hàm của các hàm số sau: y = e x . sinx

Những câu hỏi liên quan
Tính đạo hàm của các hàm số sau:
y
sin
x
-
x
.
cos
x
cos
x
+
x
.
sin
x
Đọc tiếp
Tính đạo hàm của các hàm số sau: y = sin x - x . cos x cos x + x . sin x
Tính đạo hàm của hàm số sau
y
sin
x
+
2
x
A.
cos
x
+
2
2
sin
x
+
2
x
.
B.
cos
x
+...
Đọc tiếp
Tính đạo hàm của hàm số sau y = sin x + 2 x
A. cos x + 2 2 sin x + 2 x .
B. cos x + 2 sin x + 2 x .
C. 2 2 sin x + 2 x .
D. cos x 2 sin x + 2 x .
Chọn A.
Áp dụng u / , với u = sin x + 2 x
y ' = sin x + 2 x / 2 sin x + 2 x = cos x + 2 2 sin x + 2 x .
Đúng 0
Bình luận (0)
Tính đạo hàm của hàm số sau
y
sin
x
+
cos
x
sin
x
−
cos
x
A.
−
2
sin
x
(
sin
x...
Đọc tiếp
Tính đạo hàm của hàm số sau y = sin x + cos x sin x − cos x
A. − 2 sin x ( sin x − cos x ) 2
B. 2 c osx ( sin x − cos x ) 2
C. − 2 ( sin x − cos x ) 2
D. − 2 s inx + c osx ( sin x − cos x ) 2
y ' = sin x + cos x sin x − cos x ' = ( sin x + cos x ) ' . ( sin x − cos x ) − ( sin x − cos x ) ' . ( sin x + cos x ) ( sin x − cos x ) 2 = ( cos x − sin x ) ( sin x − cos x ) − ( cos x + sin x ) ( sin x + cos x ) ( sin x − cos x ) 2 = − ( cos x − sin x ) ( − sin x + cos x ) − ( sin x + cos x ) ( sin x + cos x ) ( sin x − cos x ) 2
= − ( cos x − sin x ) 2 − ( sin x + cos x ) 2 ( sin x − cos x ) 2 = − ( cos 2 x − 2 cos x sin x + sin 2 x ) − ( sin 2 x + 2 sin x cos x + cos 2 x ) ( sin x − cos x ) 2 = − ( 1 − 2 cos x sin x ) − ( 1 + 2 sin x cos x ) ( sin x − cos x ) 2
= − 2 ( sin x − cos x ) 2
Chọn đáp án C
Đúng 0
Bình luận (0)
Tính đạo hàm của hàm số y = sinx + cos x
A. sinx + cosx
B. sinx – cosx
C. cosx – sinx
D. - sinx – cosx
y ' = ( sin x + cos x ) ' y ' = ( sin x ) ' + ( cos x ) ' = c osx - sinx
Chọn đáp án C
Đúng 0
Bình luận (0)
Tìm đạo hàm của các hàm số sau y = sin x + cos x sin x - c o s x
Tính đạo hàm của các hàm số
y = 3 x 2 - ln x + 4 . sin x
tính đạo hàm của các hàm số sau:
y=(x-1) e^2x
lớp 2 có học hàm r hả
lớp hai học hàm hả tui học lên lớp 4 rồi mà chưa học
học ở mô rứa
Xem thêm câu trả lời
Tìm đạo hàm của hàm số sau: y = sin x - x cos x cos x + x sin x
Tính đạo hàm cấp hai của hàm số
y
x
2
.
sin
x
A.
y
(
2
+
x
2
)
sin
x
+
2
x
.
cos
x
B.
y...
Đọc tiếp
Tính đạo hàm cấp hai của hàm số y = x 2 . sin x
A. y ' ' = ( 2 + x 2 ) sin x + 2 x . cos x
B. y ' ' = ( 1 - x 2 ) sin x + 6 x . cos x
C. y ' ' = ( 2 - x 2 ) sin x + 4 x . cos x
D. Đáp án khác
Ta có: y ' = 2 x . sin x + x 2 . cos x
y
'
'
=
2
sin
x
+
2
x
.
c
osx + 2x.cosx - x
2
s
inx
=
(
2
−
x
2
)
sin
x
+
4
x
.
cos
x
Chọn đáp án C
Đúng 0
Bình luận (0)
Tính đạo hàm của hàm số y = sin(cosx) + cos(sinx)
A: sin(2cosx)
B: cos(xsinx)
C: cos(2sinx)
D: -sin(x+cosx)
Chọn D.
Bước đầu tiên sử dụng đạo hàm tổng, sau đó sử dụng (sin u)’, (cos u)’.
y' = (sin(cosx))’ + (cos(sinx))’ = cos(cosx).(cosx)’ – sin(sinx).(sinx)’
= -sinx.cos(cosx) – cosx.sin(sinx) = -(sinx.cos(cosx) + cosx.sin(sinx))
= -sin(x + cosx).
Đúng 0
Bình luận (0)