Cho khối tứ diện ABCD có thể tích V. Gọi G 1 G 2 G 3 G 4 là trọng tâm của 4 mặt của tứ diện ABCD. Thể tích của khối tứ diện G 1 G 2 G 3 G 4 là
A. V 27
B. V 18
C. V 4
D. V 12
Cho hình tứ diện đều ABCD có cạnh bằng 3. Gọi G₁, G₂, G₃, G₄ lần lượt là trọng tâm của bốn mặt của tứ diện ABCD. Tính thể tích V của khối tứ diện G₁G₂G₃G₄.
A. 2 4
B. 2 18
C. 9 2 32
D. 2 12
Chọn D
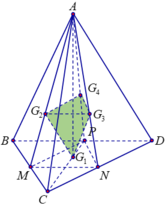
Tứ diện đều ABCD ⇒ A G 1 ⊥ B C D
Ta có ngay 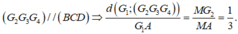
Cạnh C G 1 = B C 3 = 3 ⇒ G 1 A = A C 2 - G 1 C 2 = 6 ⇒ d G 1 ; G 2 G 3 G 4 = 6 3
Lại có G 2 G 3 M N = A G 2 A M = 2 3 ⇒ G 2 G 3 = 2 3 M N = 1 3 B D = 1
Tương tự G₃G₄=1, G₄G₂=1 ⇒ ∆ G 2 G 3 G 3 là tam giác đều có cạnh bằng 1
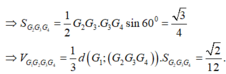
Cho tứ diện ABCD có thể tích V. Gọi G là trọng tâm tam giác ADC. Tính thể tích khối chóp G.ABC theo V.
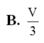
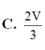
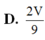
Cho tứ diện ABCD có thể tích V. Gọi G là trọng tâm tam giác ADC. Tính thể tích khối chóp G.ABC theo V.
A. V 2
B. V 3
C. 2 V 3
D. 2 V 9
Cho khối tứ diện ABCD có thể tích là V. Gọi E, F, G lần lượt là trung điểm BC, BD, CD và M, N, P, Q lần lượt là trọng tâm ∆ A B C ; ∆ A B D ; ∆ A C D ; ∆ B C D . Tính thể tích khối tứ diện MNPQ theo V.
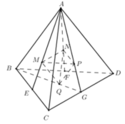
A. V 9
B. V 3
C. 2 V 9
D. V 27
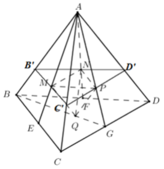
Ta có:
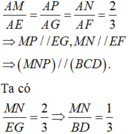
Ta có ∆ M N P đồng dạng với ∆ B C D theo tỉ số
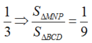
Dựng B ' C ' qua M và song song BC. C ' D ' qua P và song song với CD.
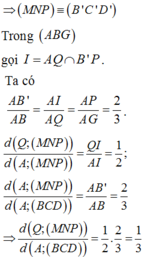

Chọn D.
Cho tứ diện đều ABCD có tất cả các cạnh bằng a. Gọi G là trọng tâm tam giác BCD. Gọi S là điểm đối xứng của G mặt phẳng (ABC). Thể tích khối đa diện SABCD là:
A. a 3 2
B. a 3 2 3
C. a 3 2 6
D. a 3 2 9
Cho tứ diện ABCD có thể tích bằng 12 và G là trọng tâm tam giác BCD. Tính thể tích V của khối chóp A.GBC.
A. V = 3
B. V = 4
C. V = 6
D. V = 5
Cho tứ diện ABCD có thể tích bằng 12 và G là trọng tâm của tam giác BCD. Tính thể tích V của khối chóp A.GBC
A. V=3
B. V=4
C. V=5
D. V=6
Chọn B.
Vì G là trọng tâm của tam giác BCD nên
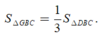
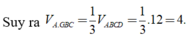
Cho tứ diện đều ABCD có tất cả các cạnh bằng a. Gọi G là trọng tâm tam giác BCD. Gọi S là điểm sao cho A S ¯ = B G ¯ . Thể tích của khối đa diện SABCD là
A. a 3 2 12
B. a 3 2 24
C. 5 a 3 2 36
D. 3 a 3 2 24
Cho tứ diện ABCD có đáy BCD là tam giác đều, trọng tâm G. ∆ là đường thẳng qua G và vuông góc với (BCD). A chạy trên ∆ sao cho mặt câu ngoại tiếp ABCD có thể tích nhỏ nhất. Khi đó thể tích khối ABCD là:
A . a 3 12
B . a 3 2 12
C . a 3 3 12
D . a 3 3 6
Đáp án A.
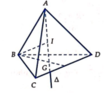
Gọi I là tâm mặt cầu ngoại tiếp ABCD => I ∈ ∆ và IA = IB = R
=> Thể tích mặt cầu ngoại tiếp ABCD nhỏ nhất ⇔ IB nhỏ nhất
![]()
![]()
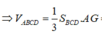
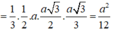
Cho tứ diện ABCD có đáy BCD là tam giác đều, trọng tâm G. ∆ là đường thẳng qua G và vuông góc với (BCD). A chạy trên ∆ sao cho mặt câu fngoaij tiếp ABCD có thể tích nhỏ nhất. Khi đó thể tích khối ABCD là
A. a 3 12
B. a 3 2 12
C. a 3 3 12
D. a 3 3 6