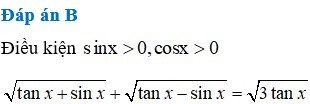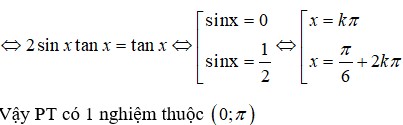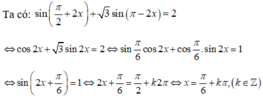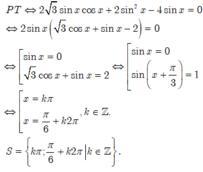Giải các phương trình tan x 2 - π 4 = tan π 8

Những câu hỏi liên quan
Giải phương trình: Tan(x-π/4) = Tan2x
\(\Leftrightarrow2x=x-\dfrac{\pi}{4}+k\pi\)
\(\Leftrightarrow x=-\dfrac{\pi}{4}+k\pi\) (\(k\in Z\))
Đúng 0
Bình luận (1)
Giải phương trình sau: tanx + tan (x+π/4) = 1
Điều kiện:
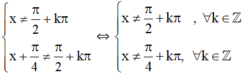
⇔ tan x.(1 - tanx) + tanx + 1 = 1 – tan x.
⇔ tan x - tan2x + 2.tan x = 0
⇔ tan2x - 3tanx = 0
⇔ tanx(tanx - 3) = 0
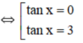
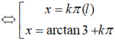
Vậy phương trình đã cho có tập nghiệm là:
{arctan 3+kπ; k ∈ Z }
Đúng 0
Bình luận (0)
Giải các phương trình: 1 - cos x = sin x x ∈ π ; 3 π
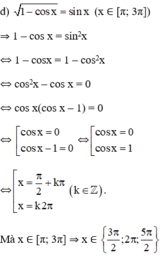
Thử lại: Trong 3 nghiệm trên thì nghiệm 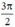 không thỏa mãn
không thỏa mãn
Đúng 0
Bình luận (0)
Phương trình
tan (
x
+
π/
3)
có nghiệm là:
Đọc tiếp
Phương trình tan ( x + π/ 3) có nghiệm là:
![]()
![]()
![]()
![]()
Số nghiệm thuộc khoảng
(
0
;
π
)
của phương trình.
tan
x
+
sin
x
+
tan
x
-
sin
x
3
tan
x
là A. 0 B. 1 C. 2 D. 3
Đọc tiếp
Số nghiệm thuộc khoảng ( 0 ; π ) của phương trình. tan x + sin x + tan x - sin x = 3 tan x là
A. 0
B. 1
C. 2
D. 3
Phương trình tan( x - π/4) = 0 có nghiệm là:
A. x = π/4 + kπ, k ∈ Z.
B. x = 3π/4 + kπ, k ∈ Z.
C. x = kπ, k ∈ Z.
D. x = k2π, k ∈ Z.
Giải các phương trình sau: sin(
π
2
+ 2x) +
3
sin(π - 2x) 2 A. x ±
π
6
+ k2π B. x ±
5
π
6
+ k2π C. x
π
4
+ k2π D. x
π
6
+ kπ
Đọc tiếp
Giải các phương trình sau: sin( π 2 + 2x) + 3 sin(π - 2x) = 2
A. x = ± π 6 + k2π
B. x = ± 5 π 6 + k2π
C. x = π 4 + k2π
D. x = π 6 + kπ
Giải các phương trình sau. π 1. 2sin( x − ) − 2 = 0 . 4 2. sin 2 x − 2 3 sin 2 x − cos x + 3 sin x = 0 .
giúp em với adim
lớp 11
Cho phương trình:
3
sin
2
x
-
cos
2
x
4
sin
x
-
1
. Tổng các nghiệm trong khoảng
-
π
;
π
của phương trình là: A.
π
B.
π
6
C.
-
2
π
3
D.
-...
Đọc tiếp
Cho phương trình: 3 sin 2 x - cos 2 x = 4 sin x - 1 . Tổng các nghiệm trong khoảng - π ; π của phương trình là:
A. π
B. π 6
C. - 2 π 3
D. - π
giải phương trình sau: 2sinx-1=0 biết xϵ(-π/2: π)
\(2sinx-1=0\Leftrightarrow sinx=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
Do \(x\in\left(-\dfrac{\pi}{2};\pi\right)\Rightarrow x=\left\{\dfrac{\pi}{6};\dfrac{5\pi}{6}\right\}\)
Đúng 1
Bình luận (0)