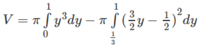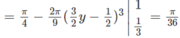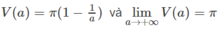Tính thể tích các khối tròn xoay tạo thành khi quay hình phẳng xác định bởi y = 1 x - 1 , y = 0, y = 2x, quanh trục Ox

Những câu hỏi liên quan
Tính thể tích các khối tròn xoay tạo thành khi quay hình phẳng xác định bởi y = |2x – x2|, y = 0 và x = 3 , quanh :
• Trục Ox
• Trục Oy
Tính thể tích các khối tròn xoay tạo thành khi quay hình phẳng xác định bởi
y
x
2
3
, x 0 và tiếp tuyến với đường
y
x
2
3
tại điểm có hoành độ x 1, quanh trục...
Đọc tiếp
Tính thể tích các khối tròn xoay tạo thành khi quay hình phẳng xác định bởi y = x 2 3 , x = 0 và tiếp tuyến với đường y = x 2 3 tại điểm có hoành độ x = 1, quanh trục Oy;
Tính thể tích khối tròn xoay tạo bởi phép quay quanh trục Ox hình phẳng giới hạn bởi các đường , y 0, x 1 và x a (a 1). Gọi thể tích đó là V(a). Xác định thể tích của vật thể khi a → +
∞
(tức là ).
Đọc tiếp
Tính thể tích khối tròn xoay tạo bởi phép quay quanh trục Ox hình phẳng giới hạn bởi các đường 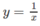 , y = 0, x = 1 và x = a (a > 1). Gọi thể tích đó là V(a). Xác định thể tích của vật thể khi a → +
∞
(tức là
, y = 0, x = 1 và x = a (a > 1). Gọi thể tích đó là V(a). Xác định thể tích của vật thể khi a → +
∞
(tức là 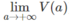 ).
).
Tính thể tích khối tròn xoay tạo bởi phép quay quanh trục Ox hình phẳng giới hạn bởi các đường y
1
x
, y 0, x 1 và x a (a 1). Gọi thể tích đó là V(a). Xác định thể tích của vật thể khi a → +
∞
(tức là
lim
a
→
+
∞
V...
Đọc tiếp
Tính thể tích khối tròn xoay tạo bởi phép quay quanh trục Ox hình phẳng giới hạn bởi các đường y = 1 x , y = 0, x = 1 và x = a (a > 1). Gọi thể tích đó là V(a). Xác định thể tích của vật thể khi a → + ∞ (tức là lim a → + ∞ V a ).
Tính thể tích các khối tròn xoay khi quay hình phẳng xác định bởi: y = 2 – x 2 , y = 1 , quanh trục Ox.
Gọi (D) là hình phẳng giới hạn bởi các đường
y
2
x
,
y
0
,
x
0
v
à
x
2
. Thể tích V của khối tròn xoay tạo thành khi quay (D) quanh trục Ox được xác định bởi công thức: A.
V
π
∫
0
2...
Đọc tiếp
Gọi (D) là hình phẳng giới hạn bởi các đường y = 2 x , y = 0 , x = 0 v à x = 2 . Thể tích V của khối tròn xoay tạo thành khi quay (D) quanh trục Ox được xác định bởi công thức:
A. V = π ∫ 0 2 2 x + 1 d x
B. V = ∫ 0 2 2 x + 1 d x
C. V = ∫ 0 2 4 x d x
D. V = π ∫ 0 2 4 x d x
Đáp án D
Phương pháp:
Công thức tính thể tích hình phẳng được giới hạn bởi các đường thẳng x = a , x = b ( a < b ) và các đồ thị hàm số ư
y = f(x), y = g(x) khi quay quanh trục Ox là: V = π ∫ a b f 2 x - g 2 x dx
Cách giải:
Ta có công thức tính thể tích hình phẳng đã cho là:
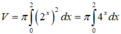
Đúng 0
Bình luận (0)
Tính thể tích các khối tròn xoay khi quay hình phẳng xác định bởi: y = 2x – x 2 , y = x , quanh trục Ox.
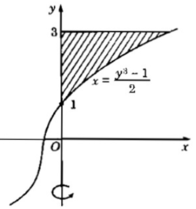
Tính thể tích các khối tròn xoay khi quay hình phẳng xác định bởi: y = 2 x + 1 1 3 ,x = 0, y = 3, quanh trục Oy.
Cho hình phẳng (H) giới hạn bởi các đường
y
ln
2
x
+
1
,
y
0
,
x
0
,
x
1
. Tính thể tích của khối tròn xoay tạo thành khi quay hình (H) quanh trục Ox. A.
3
2
ln
3
-...
Đọc tiếp
Cho hình phẳng (H) giới hạn bởi các đường y = ln 2 x + 1 , y = 0 , x = 0 , x = 1 . Tính thể tích của khối tròn xoay tạo thành khi quay hình (H) quanh trục Ox.
A. 3 2 ln 3 - 1
B. π 2 ln 3 - π
C. π + 1 2 ln 3 - 1
D. 3 π 2 ln 3 - π
HD: Thể tích của khối tròn xoay tạo thành khi quay hình (H) quanh trục Ox là:
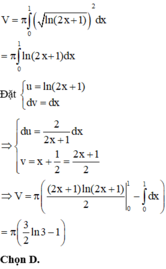
Đúng 0
Bình luận (0)