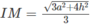Cho lăng trụ tam giác đều ABC.A’B’C’, cạnh đáy bằng a. Gọi N, I lần lượt là trung điểm của AB, BC; góc giữa hai mặt phẳng (C’AI) và (ABC) bằng 60°. Tính theo a thể tích khối chóp NAC’I?
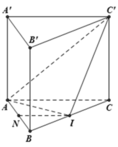
A. 32 a 3 3
B. a 3 32
C. a 3 3 32
D. a 3 3 4
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có cạnh bằng a và chiều cao bằng 2a. Gọi M, N lần lượt là trung điểm của BC và A’C’
A. 2a
B. a 3
C. a
D. a
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có cạnh bằng a và chiều cao bằng 2a. Gọi M, N lần lượt là trung điểm của BC và A’C’
A. 2a
B. a 3
C. a
D. a 2
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có A B = 2 3 và AA’= 2. Gọi M, N, P lần lượt là trung điểm của các cạnh A’B’, A’C’ và BC. Côsin của góc tạo bởi hai mặt phẳng (AB’C’) và (MNP) bằng:
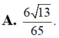
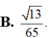
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có A B = 2 3 và AA’=2. Gọi M,N,P lần lượt là trung điểm của các cạnh A’B’, A’C’ và BC. Côsin của góc tạo bởi hai mặt phẳng (AB’C’) và (MNP) bằng
A. 6 13 65
B. 13 65
C. 17 13 65
D. 18 63 65
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có A B = 2 3 và AA’=2. Gọi M,N,P lần lượt là trung điểm của các cạnh A’B’, A’C’ và BC. Côsin của góc tạo bởi hai mặt phẳng (AB’C’) và (MNP) bằng
A. 6 13 65
B. 13 65 .
C. 17 13 65 .
D. 18 63 65 .
Đáp án B.

Dễ thấy:
A B ' C ' ; M N P ^ = A B ' C ' ; M N C B ^
= 180 0 − A B ' C ' ; A ' B ' C ' ^ − M N B C ; A ' B ' C ' ^ = 180 0 − A ' B C ; A B C ^ − M N B C ; A B C . ^
Ta có:
M N B C ; A B C ^ = A ' P ; A P ^ = A ' P A ^ = arctan 2 3 .
Và
M N B C ; A B C ^ = S P ; A P ^ = S P A ^ = arctan 4 3 ,
với S là điểm đối xứng với A qua A’,
thì S A = 2 A A ' = 4.
Suy ra
cos A B ' C ' ; M N P ^ = c os 180 0 -arctan 2 3 − arctan 4 3 = 13 65 .
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại B, AB = 4, BC = 6 và AA’ = 10. Gọi K, M, N lần lượt là trung điểm của các cạnh BB’, A’B’, BC. Thể tích khối tứ diện C’KMN là:
A. 15
B. 45
C. 5
D. 10
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng a, góc giữa hai mặt phẳng (A’BC) và (ABC) bằng 60 o . Gọi M là trung điểm cạnh BC, N là trung điểm CC’. Tính thể tích khối chóp A.BB’C’C
A. a 3 3 4
B. a 3 3 2
C. a 3 3 8
D. a 3 3 6
Do tam giác ABC đều cạnh a và M là trung điểm BC cho nên A M ⊥ B C và A M = a 3 2 .
A M ⊥ B C và A A ' ⊥ B C ⇒ A ' M ⊥ B C
⇒ Góc giữa hai mặt phẳng (A’BC) và (ABC) là A ' M A ^ = 60 o
Tam giác A’AM vuông góc tại A nên A A ' = A M . tan 60 o = a 3 2 . 3 = 3 a 2
Diện tích hình chữ nhật BB’C’C là S B B ' C ' C = B B ' . B C = 3 a 2 2
A M ⊥ B C và A M ⊥ B B ' ⇒ A M ⊥ B B ' C ' C
Thể tích khối chóp A.BB’C’C là: V = 1 3 . S B B ' C ' C . A M = 1 3 . 3 a 2 2 . a 3 2 = a 3 3 4 (đvtt).
Đáp án A
Cho lăng trụ đứng tam giác đều ABC.A’B’C’ có cạnh đáy bằng a. Gọi I là trung điểm của B’C’. Tính khoảng cách từ điểm B tới mặt phẳng (AA’I)
A. a/3
B. a
C. a/2
D. a/4
Cho lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng a và có đường cao h. Gọi I là trung điểm của cạnh BC. Đường thẳng A’I cắt hình trụ nội tiếp nói trên theo một đoạn thẳng. Tính độ dài đoạn thẳng đó.
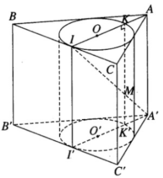
Ta có mặt phẳng (AA’I) là mặt phẳng qua trục hình trụ. Mặt phẳng này cắt hình trụ theo thiết diện là hình chữ nhật IKK’I’. Đoạn A’I cắt KK’ tại M nên cắt hình trụ theo đoạn IM.
Ta có:
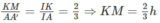
Xét tam giác vuông IKM ta có:
IM 2 = IK 2 + KM 2
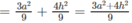
Vậy