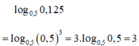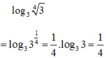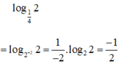Sử dụng máy tính cầm tay, tính giá trị các biểu thức sau (làm tròn kết quả đến chữ số thập phân thứ tư):

a) \({\log _3}15\);

b) \(\log 8 - \log 3\);

c) \(3\ln 2\).

Không dùng máy tính cầm tay, hãy tính \({\log _9}\frac{1}{{27}}.\)

a/ Không sử dụng máy tính .Cho góc nhọn α , biết sinα = \(\dfrac{\sqrt{3}}{2}\) . Hãy tính cosα ; tanα ; cotα.

b/ Không sử dụng máy tính .Cho góc nhọn α , biết cosα = \(\dfrac{\sqrt{5}}{7}\) . Hãy tính cosα ; tanα ; cotα.

Sử dụng máy tính cầm tay, tính giá trị các biểu thức sau (làm tròn kết quả đến chữ số thập phân thứ sáu):

a) \({\log _5}0,5\);                 

b) \(\log 25\);                       

c) \(\ln \frac{3}{2}\).

Xét phương trình \(2{\log _2}x =  - 3.\)

a) Từ phương trình trên, hãy tính \({\log _2}x.\)

b) Từ kết quả ở câu a và sử dụng định nghĩa lôgarit, hãy tìm x.

Không sử dụng máy tính, hãy tính:  log 0 , 5 0 , 125

Không sử dụng máy tính, hãy tính:  log 3 3 4

Không sử dụng máy tính, hãy tính:  log 1 4 2

Không sử dụng máy tính, hãy tính:

a) \({( - 3)^8}\) biết \({( - 3)^7} =  - 2187\)

b) \({\left( { - \frac{2}{3}} \right)^{12}}\) biết \({\left( { - \frac{2}{3}} \right)^{11}} = \frac{{ - 2048}}{{177147}}\)