Giá trị của m để phương trình (m - 1) x 2 - (2m - 2)x + 2m = 0 vô nghiệm là:
A. [ m ≥ 2 m < - 2
B. [ m ≥ 3 m < - 3
C. [ m ≥ 1 m < - 1
D. [ m ≥ 4 m < - 4
Tìm các giá trị của m để bất phương trình sau vô nghiệm:
f(x) = (m + 1) x 2 - 2(3 - 2m)x + m + 1 ≥ 0
f(x) = (m + 1) x 2 - 2(3 - 2m)x + m + 1 ≥ 0 (1)
Với m = -1:
(1) ⇔ -10x ≥ 0 ⇔ x ≤ 0
Vậy với m = -1 bất phương trình (1) có nghiệm x ≤ 0
Suy ra, m = -1 (loại)
Với m ≠ -1:
f(x) = (m +1 ) x 2 - 2(3 - 2m)x + m + 1
Δ' = [-(3 - 2m) ] 2 - (m + 1)(m + 1) = (2m - 3 ) 2 - (m + 1 ) 2
= (2m - 3 + m + 1)(2m - 3 - m - 1) = (3m - 2)(m - 4)
Để bất phương trình (1) vô nghiệm thì:
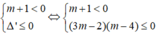
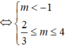
Vậy không có giá trị nào của m để bất phương trình (1) vô nghiệm
Gọi n là số các giá trị của tham số m để bất phương trình ( 2 m - 4 ) ( x 3 + 2 x 2 ) + ( m 2 - 3 m + 2 ) - ( m 3 – m 2 - 2 m ) ( x + 2 ) < 0 vô nghiệm. Giá trị của n bằng
A. 5
B. 1
C. 4
D. 2
Tìm tất cả các giá trị của m để bất phương trình vô nghiệm m + 1 x 2 + 2 ( m - 2 ) + 2 m - 4 - x 2 + x - 2 ≥ 0
![]()
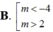
![]()
![]()
a Tìm m để phương trình vô nghiệm: x2 - (2m - 3)x + m2 = 0.
b Tìm m để phương trình vô nghiệm: (m - 1)x2 - 2mx + m -2 = 0.
c Tìm m để phương trình vô nghiệm: (2 - m)x2 - 2(m + 1)x + 4 - m = 0
\(a,x^2-\left(2m-3\right)x+m^2=0-vô-ngo\)
\(\Leftrightarrow\Delta< 0\Leftrightarrow[-\left(2m-3\right)]^2-4m^2< 0\Leftrightarrow m>\dfrac{3}{4}\)
\(b,\left(m-1\right)x^2-2mx+m-2=0\)
\(m-1=0\Leftrightarrow m=1\Rightarrow-2x-1=0\Leftrightarrow x=-0,5\left(ktm\right)\)
\(m-1\ne0\Leftrightarrow m\ne1\Rightarrow\Delta'< 0\Leftrightarrow\left(-m\right)^2-\left(m-2\right)\left(m-1\right)< 0\Leftrightarrow m< \dfrac{2}{3}\)
\(c,\left(2-m\right)x^2-2\left(m+1\right)x+4-m=0\)
\(2-m=0\Leftrightarrow m=2\Rightarrow-6x+2=0\Leftrightarrow x=\dfrac{1}{3}\left(ktm\right)\)
\(2-m\ne0\Leftrightarrow m\ne2\Rightarrow\Delta'< 0\Leftrightarrow[-\left(m+1\right)]^2-\left(4-m\right)\left(2-m\right)< 0\Leftrightarrow m< \dfrac{7}{8}\)
Tìm các giá trị của tham số m để phương trình sau vô nghiệm (m - 2)x2 + 2(2m - 3)x + 5m - 6 = 0
(m - 2)x2 + 2(2m - 3)x + 5m - 6 = 0 (1)
- Nếu m - 2 = 0 ⇔ m = 2, khi đó phương trình (1) trở thành:
2x + 4 = 0 ⇔ x = -2 hay phương trình (1) có một nghiệm
Do đó m = 2 không phải là giá trị cần tìm.
- Nếu m - 2 ≠ 0 ⇔ m ≠ 2 ta có:
Δ' = (2m - 3)2 - (m - 2)(5m - 6)
= 4m2 - 12m + 9 - 5m2 + 6m + 10m - 12
= -m2 + 4m - 3 = (-m + 3)(m - 1)
(1) vô nghiệm ⇔ Δ' < 0 ⇔ (-m + 3)(m - 1) < 0 ⇔ m ∈ (-∞; 1) ∪ (3; +∞)
Vậy với m ∈ (-∞; 1) ∪ (3; +∞) thì phương trình vô nghiệm.
Tìm giá trị của tham số m để phương trình sau vô nghiệm:\(\dfrac{x^2}{4}+\left(2m+1\right)x+5m^2+3m+16=0\)
Pt vô nghiệm khi:
\(\Delta=\left(2m+1\right)^2-\left(5m^2+3m+16\right)< 0\)
\(\Leftrightarrow-m^2+m-15< 0\) (luôn đúng)
Vậy pt đã cho vô nghiệm với mọi m
tìm giá trị của m để phương trình vô nghiệm x/x-m-2m/x+m=8m^2/x^2-m^2
Tìm các giá trị của tham số m để phương trình m x 2 + 2 ( 2 m - 1 ) x + m + 2 = 0 vô nghiệm
A. 3 - 6 3 < m < 3 + 6 3
B. Không tồn tại m
C. m < 1/12
D. m ≠ 0; m < 1/12
Cho phương trình \(x^2-\left(2m-1\right)x+2m-2=0\)
Gọi \(x_1\),\(x_2\) là 2 nghiệm của phương trình. Tìm giá trị của m để biểu thức \(A=x_1^2+x_2^2\) đạt giá trị nhỏ nhất.
\(\Delta=4m^2-4m+1-4\left(2m-2\right)=4m^2-12m+9=\left(2m-3\right)^2\ge0\)
Do đó pt luôn có nghiệm
Theo định lí Vi-ét:
\(\left\{{}\begin{matrix}x_1+x_2=2m-1\\x_1x_2=2m-2\end{matrix}\right.\)
Lại có: \(A=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2\)
\(A=\left(2m-1\right)^2-2\left(2m-2\right)\)
\(A=4m^2-4m+1-4m+4\)
\(A=4m^2-8m+5\)
\(A=4\left(m-1\right)^2+1\ge1\)
Dấu "=" xảy ra \(\Leftrightarrow\) m=1
Tick hộ nha 😘
pt có nghiệm \(< =>\Delta\ge0\)
\(< =>[-\left(2m-1\right)]^2-4\left(2m-2\right)\ge0\)
\(< =>4m^2-4m+1-8m+8\ge0\)
\(< =>4m^2-12m+9\ge0\)
\(< =>4\left(m^2-3m+\dfrac{9}{4}\right)\ge0\)
\(=>m^2-2.\dfrac{3}{2}m+\dfrac{9}{4}\ge0< =>\left(m-\dfrac{2}{3}\right)^2\ge0\)(luôn đúng)
=>pt luôn có 2 nghiệm
theo vi ét \(=>\left\{{}\begin{matrix}x1+x2=2m-1\\x1x2=2m-2\end{matrix}\right.\)
\(A=\left(x1+x2\right)^2-2x1x2=\left(2m-1\right)^2-2\left(2m-2\right)\)
\(A=4m^2-4m+1-4m+4=4m^2+5\ge5\)
dấu"=" xảy ra<=>m=0
\(\Delta=\left(2m-1\right)^2-4\left(2m-2\right)=4m^2-12m+9=\left(2m-3\right)^2\ge0;\forall m\)
\(\Rightarrow\) Phương trình đã cho luôn có nghiệm
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m-1\\x_1x_2=2m-2\end{matrix}\right.\)
\(A=\left(x_1+x_2\right)^2-2x_1x_2\)
\(A=\left(2m-1\right)^2-2\left(2m-2\right)\)
\(A=4m^2-8m+5=4\left(m-1\right)^2+1\ge1\)
Dấu "=" xảy ra khi \(m-1=0\Leftrightarrow m=1\)