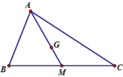
Cho tam giác ABC với trung tuyến AM và trọng tâm G. Khi đó A G → bằng
A. 1 2 G M →
B. - 1 3 A M →
C. 2 3 A M →
D. - 2 3 A M →
cho tam giác ABC coa đường trung tuyến AM và trọng tâm G . khi đó tỉ soo GM/AG bằng :
A, 1/3
B,2/3
C,1/2
D,2
cho tam giác ABC coa đường trung tuyến AM và trọng tâm G . khi đó tỉ soo GM/AG bằng :
A, 1/3
B,2/3
C,1/2
D,2
Theo định lý trọng tâm của đường trung tuyến:
`-` Trọng tâm của tam giác cách đỉnh `2/3,` cách đáy `1/3`
Vì `G` là trọng tâm của tam giác `ABC -> AG=2/3 AM, GM=1/3 AM`
`->` Tỉ số của \(\dfrac{GM}{AG}=\dfrac{\left(\dfrac{1}{3}\right)}{\left(\dfrac{2}{3}\right)}=\dfrac{1}{2}\)
`-> C`
Cho tam giác ABC với trung tuyến AM và trọng tâm G. Khi đó G A → =
A. 2 G M →
B. 2 3 G M →
C. - 2 3 A M →
D. 1 2 A M →
Cho tam giác ABC với trung tuyến AM và trọng tâm G. Khi đó G A → =
![]()
![]()
![]()
![]()
Chọn C.
Ta có 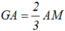 .Mặt khác
.Mặt khác ![]() và
và ![]() ngược hướng =>
ngược hướng =>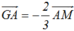 .
.
1) tam giác ABC có các đường trung tuyến BD và CE bằng nhau . chứng minh rằng tam giác ABC là tam giác cân.
2)cho tam giác ABC cân ở A , AB=34cm , BC =32cm , và 3 trung tuyến AM , BN , CP đồng quy tại trọng tâm G
a) chúng minh AM vuông góc với
b) tính độ dài AM , BN ,CP (làm trong kết quả đến chữ số thập phân thứ 2)
câu 2 :
a) có phải là chứng minh AM ⊥ BC không
xét ΔAMB và ΔAMC, ta có :
AB = AC (2 cạnh bên của ΔABC cân tại A)
MB = MC (AM là đường trung tuyến của cạnh BC)
AM là cạnh chung
=> ΔAMB = ΔAMC (c.c.c)
=> \(\widehat{AMB}=\widehat{AMC}\) (2 cạnh tương ứng)
mà \(\widehat{AMB}+\widehat{AMC}=180^O\) (kề bù)
\(\Rightarrow\widehat{AMB}=\widehat{AMC}=\dfrac{180^O}{2}=90^O\)
=> AM ⊥ BC
Cho tam giác ABC trung tuyến AM, điểm G trọng tâm. Chứng minh trung tuyến AM đi qua G (A, G, M thẳng hàng).
Trả lời nhanh mình chấm đúng cho
Cho tam giác ABC, đường trung tuyến AM và trọng tâm G. Gọi I là điểm đối xứng với A qua G. CMR: I đối xứng với G qua M.
\(AG=\frac{2}{3}AM=IG\)
\(MG=\frac{1}{3}AM\) mà \(IM=IG-MG=\frac{2}{3}AM-\frac{1}{3}AM=\frac{1}{3}AM\)
\(\Rightarrow MG=IM=\frac{1}{3}AM\) => I đối xứng với G qua M
Bài 1:Cho tam giác ABC, trung tuyến AM, trọng tâm G. I, K thuộc tia đối AM sao cho MI=MG, IK=IG. N là tủng điểm của CK.
Chứng minh: B, I, N thẳng hàng.
Bài 2: G là trọng tâm của tam giác ABC, G' thuộc AG sao cho G là trung điểm của AG'.
a) So sánh các cạnh của tam giác BGG' với các đường trung tuyến của tam giác ABC.
b) So sánh các đường trung tuyến của tam giac BGG' với các cạnh của tam giac ABC.
Giải chi tiết nhá m.n. Tks m.n trước :)
Cho tam giác ABC, đường trung tuyến AM và trọng tâm G. Gọi I là điểm đối xứng với A qua G. Chứng minh rằng I là điểm đối xứng với G qua M.
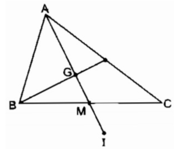
I đối xứng với A qua tâm G
ta có: GA = GI, GM ∈ GA ( tính chất đường trung tuyến của tam giác)
Suy ra: GM ∈ GI
Mà: GM + MI = GI và GM = AG/2 (tính chất đường trung tuyến) =>GM = GI/2
Suy ra: GM = MI nên điểm M là trung điểm của GI
Vậy I đối xứng với G qua M.
Cho tam giác ABC có đường trung tuyến AD và trọng tâm G khi đó tỉ số AG: AD bằng
tỉ số giữa AG và AD
\(\dfrac{AG}{AD}=\dfrac{2}{3}\)
bạn tự vẽ hình bài này nhé
Có `G` là trọng tâm `Delta ABC`
`=>AG=2/3 AD(t/c)`
hay `(AG)/(AD)=2/3`