Giới hạn bên phải của hàm số y = 3 x - 7 x - 2 khi x → 2 là:
A. + ∞
B. - ∞
C. 3
D. 7 2
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số y = − 3 x 2 + x + 4 và trục hoành. Gọi S 1 v à S 2 lần lượt là diện tích phần hình (H) nằm bên trái và bên phải trục tung. Tính tỉ số S 1 S 2 .
A. S 1 S 2 = 135 208 .
B. S 1 S 2 = 135 343 .
C. S 1 S 2 = 208 343 .
D. S 1 S 2 = 54 343 .
Phương pháp:
Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số
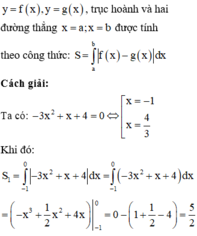
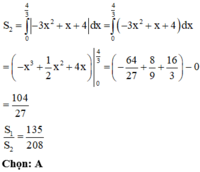
Viết công thức tính diện tích S của hình phẳng (H) giới hạn bởi các đồ thị hàm số y = f x , y = g x và hai đường thẳng x = a , x = b (như hình vẽ bên).

A. S = ∫ a c f x - g x d x + ∫ c b g x - f x d x
B. S = ∫ a c g x - f x d x + ∫ c b f x - g x d x
C. S = ∫ a b g x - f x d x
D. S = ∫ a b f x - g x d x
Cho hàm số y = f ( x ) liên tục trên đoạn [a;b] có đồ thị như hình bên và c ∈ a ; b . Gọi S là diện tích của hình phẳng (H) giới hạn bởi đồ thị hàm số y = f ( x ) và các đường thẳng y = 0 , x = a , x = b . . Mệnh đề nào sau đây sai?
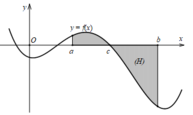
A. S = ∫ a c f x d x + ∫ c b f x d x
B. S = ∫ a c f x d x − ∫ c b f x d x
C. S = ∫ a b f x d x
D. S = ∫ a c f x d x + ∫ b c f x d x
Cho hàm số f x = 7 − 4 x 2 k h i 0 ≤ x ≤ 1 4 − x 2 k h i x > 1 . Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số f x và các đường thẳng x = 0 , x = 3 , y = 0
A. 16 3
B. 20 3
C. 10
D. 9
Phương pháp:
Công thức tính diện tích hình phẳng được giới hạn bởi các đường thẳng

Tìm giới hạn của hàm số sau:
\(\lim\limits_{x\rightarrow1}\dfrac{\sqrt{2x+7}-3}{x-1}\)
\(\left(...\right)=\lim\limits_{x\rightarrow1}\dfrac{2\left(x-1\right)}{\left(x-1\right)\left(\sqrt{2x+7}+3\right)}=\lim\limits_{x\rightarrow1}\dfrac{2}{\sqrt{2x+7}+3}=\dfrac{1}{3}\)
Cho đồ thị hàm số y=f(x) đi qua gốc tọa độ O, ngoài ra còn cắt trục Ox tại các điểm có hoành độ lần lượt bằng ‒3 và 4 như hình bên. Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số và trục Ox.
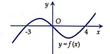
A. S = ∫ − 3 4 f x d x
B. S = ∫ − 3 0 f x d x + ∫ 0 4 f x d x
C. S = ∫ − 3 0 f x d x + ∫ 4 0 f x d x
D. S = ∫ 0 - 3 f x d x + ∫ 0 4 f x d x
Hình phẳng (H) được giới hạn bởi đồ thị của hai hàm số đa thức bậc bốn y=f(x) và y=g(x). Biết rằng đồ thị của hai hàm số này cắt nhau tại đúng ba điểm phân biệt có hoành độ lần lượt là −3;−1;2. Diện tích của hình phẳng (H) (phần gạch sọc trên hình vẽ bên) gần nhất với kết quả nào dưới đây?
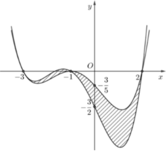
A.3,11
B. 2,45
C. 3,21
D. 2,95
Cho hàm số y = x 2 = 5 x + 7 ( C 1 ) , y = x + k ( C 2 ) , gọi H là hình phẳng giới hạn bới ( C 1 , C 2 ). Để diện tích (H) bằng 32/3 thì giá trị của k bằng
A. 1
B. 2
C. 3
D. 4
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành, đường thẳng x = a, x = b(như hình bên).
Hỏi cách tính S nào dưới đây đúng?
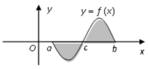
A. S = ∫ a b f x d x .
B. S = ∫ a c f x d x + ∫ c b f x d x .
C. S = − ∫ a c f x d x + ∫ c b f x d x .
D. S = ∫ a c f x d x + ∫ c b f x d x .