Cho hình bình hành ABCD. A B → + A C → + A D → Tổng các vectơ là
A. A C →
B. 2
C . 3
D. 5
Cho hình bình hành ABCD với A(2;3;-2), B(1;1;-3), C(-2;0;5), D(-1;3;4). Diện tích của hình bình hành ABCD bằng:
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz cho hình bình hành ABCD. Biết A(2;1;-3), B(0;-2;5) và C(1;1;3). Diện tích hình bình hành ABCD là
A. 2 87
B. 349 2
C. 349
D. 87
Đáp án C
Giả sử D(a;b;c).Vì ABCD là hình bình hành nên
![]()
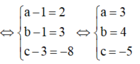
![]()
Diện tích hình bình hành ABCD là
![]()
Cho hình bình hành ABCD với A(2; 4; -2), B(1; 1; -3), C(-2; 0; 5), D(-1; 3; 4). Diện tích của hình bình hành ABCD bằng:
A. 245 đvdt
B. 615 đvdt
C. 2 731 đvdt
D. 345 đvdt
Cho hình bình hành ABCD. Vẽ AH,CK \(\perp\)BD
a) C/m AHCK là hình bình hành
b) AH, CK cắt cạnh hình bình hành tại M, N. C/m tâm O của hình bình hành ABCD là trung điểm của MN
Hình em tự vẽ nha.
a, ABCD là hình bình hành \(\Rightarrow\)2 đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường
Tứ giác AHCK có 2 đường chéo AC và HK tại trung điểm của mỗi đường \(\Rightarrow\)AHCK là hình bình hành
b, AHCK là hình bình hành \(\Rightarrow AH//CK\Leftrightarrow AM//NC\)
Tứ giác AMCN có: \(AN//MC\left(gt\right)\)
\(AM//NC\left(cmt\right)\)
\(\Rightarrow\)AMCN là hình bình hành \(\Rightarrow\)2 đường chéo AC và MN cắt nhau tại trung điểm O của AC \(\Rightarrow\)O là trung điểm của MN
Cho hình bình hành ABCD. Vẽ AH,CK vuông góc với đường chéo BD
a) C/m AHCK là hình bình hành
b)Gọi O là giao điểm của AC và BD. CM: 3 điểm H, K, O thẳng hàng
Cho hình bình hành ABCD. Vẽ AH,CK \(\perp\)BD
a) C/m AHCK là hình bình hành
b) AH, CK cắt cạnh hình bình hành tại M, N. C/m tâm O của hình bình hành ABCD là trung điểm của MN
câu 10 cho hình bình hành ABCD (AB//GÓC D=130\(^0\)
CD và góc B - góc C =50\(^0\)hãy tính các góc còn lại của hình thang
câu 11 cho hình bình hành ABCD có góc A =3 lần góc B.Hãy tính số đo góc của hình bình hành
Câu 10:
góc A=180-130=50 độ
góc B=(180+50)/2=230/2=115 độ
góc C=180-115=65 độ
Cho hình bình hành ABCD. Gọi E, F lần lượt là hình chiếu của A, C trên BD. a) Chứng minh: AE = CF b) Chứng minh AECF là hình bình hành
a: Xét ΔADE vuông tại E và ΔCBF vuông tại F có
AD=CB
\(\widehat{ADE}=\widehat{CBF}\)
Do đó: ΔADE=ΔCBF
Suy ra: AE=CF
b: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
Cho hình bình hành ABCD. Đường thẳng d nằm ngoài hình bình hành. Gọi A', B', C', D' lần lượt là hình chiếu của A,B,C,D lên d. Chứng minh AA' + CC' = BB' + DD'
Cho 3 điểm A(2,5), B(1,1), C(3,3) . Tìm tọa độ điểm D sao cho ABCD là hình bình hành. Tìm tọa độ tâm hình bình hành.
\(\overrightarrow{AB}=\left(-1;-4\right)\)
Ta có: ABCD là hình bình hành
nên \(\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Leftrightarrow\overrightarrow{DC}=\left(-1;-4\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_D-3=-1\\y_D-3=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_D=2\\y_D=-1\end{matrix}\right.\)
Cho hình bình hành ABCD các tia phân giác của các góc của hình bình hành cắt nhau tạo thành tứ giác EFGH. CMR:
a, Tứ giác EFGH là hình gì? Vì sao?
b, EG = FH và bằng hiệu giữa hai cạnh kề của hình bình hành ABCD
c, Hình bình hành ABCD cần điều kiện gì để EFGH là hình vuông?