Tiếp tuyến của đồ thị hàm số y = x 3 3 + 3 x 2 - 2 có hệ số góc k = -9 có phương trình là:
A. y = -9x-11
B. y = -9x+3
C. y = -9x+43
D. y = -9x+23
Cho hàm số \(y = {x^3} - 3{{\rm{x}}^2}\). Tiếp tuyến với đồ thị của hàm số tại điểm \(M\left( { - 1;4} \right)\) có hệ số góc bằng:
A. ‒3.
B. 9.
C. ‒9.
D. 72.
Ta có: \(y'3x^2-3.2x=3x^2-6x\).
Tiếp tuyến với đồ thị của hàm số tại điểm \(M\left(-1;4\right)\) có hệ số góc bằng:\(y'\left(-1\right)=3.\left(-1\right)^2-6.\left(-1\right)=9\).
\(\Rightarrow B\)
a) tìm hệ số góc của tiếp tuyến của đồ thị hàm số y=-x^3+3x-2 (c) tại điểm có hoành độ -3
b) viết phương trình tiếp tuyến của đồ thị hàm số (c) trên tại điểm ( ứng với tiếp điểm ) có hoành độ -3
Tiếp tuyến của đồ thị hàm số y = x 3 − 3 x 2 − 2 có hệ số góc k=-3 có phương trình là:
A. y = − 3 x − 7
B. y = − 3 x + 7
C. y = − 3 x + 1
D. y = − 3 x − 1
Đáp án C
Ta có:
y ' = 3 x 2 − 6 x ⇒ y ' ( x ) = − 3 ⇔ 3 x 2 − 6 x + 3 = 0 ⇔ x = 1 ⇒ y = − 2
Viết phương trình tiếp tuyến của đồ thị hàm số:
\(y=x^3-6x+5\)
a, Tại điểm có hoành độ \(x_0=1\)
b, Tại điểm có tung độ \(y_0=5\)
c, Hệ số góc \(k=-9\)
a: y'=3x^2-6
f(1)=1-6+5=0
f'(1)=3-6=-3
y-f(1)=f'(1)(x-1)
=>y-0=-3(x-1)
=>y=-3x+3
b: y=5
=>x^3-6x=0
=>x=0 hoặc x=căn 6 hoặc x=-6
TH1: x=0
y=5; y'=3*0^2-6=-6
Phương trình sẽ là:
y-5=-6(x-0)
=>y=-6x+5
TH2: x=căn 6
y=5; y'=3*6-6=12
Phương trình sẽ là:
y-5=12(x-căn 6)
=>y=12x-12căn 6+5
TH3: x=-căn 6
y=5; y'=12
Phương trình sẽ là:
y-5=12(x+căn 6)
=>y=12x+12căn 6+5
Cho hàm số f(x) = x3 – 3x2, tiếp tuyến của đồ thị có hệ số góc k=-3 là
A. y=-3x + 1
B. y=-3x + 5
C. y=-3x - 1
D. y=-3x - 5
Cho hàm số y = x 3 3 + 3 x 2 − 2 có đồ thị C . Viết phương trình tiếp tuyến của C biết tiếp tuyến có hệ số góc k = − 9
A. y + 16 = − 9 x + 3
B. y − 16 = − 9 x − 3
C. y − 16 = − 9 x + 3
D. y = − 9 x + 3
Đáp án C
Gọi phương trình tiếp tuyến của C có dạng y − y 0 = y ' x 0 x − x 0
Ta có y ' x 0 = x 0 2 + 6 x 0
suy ra
y ' x 0 = − 9 ⇔ x 0 2 + 6 x 0 + 9 = 0 ⇔ x 0 = − 3 → y 0 = 16
Vậy phương trình tiếp tuyến cần tìm là
y − 16 = − 9 x + 3 ⇔ y = − 9 x − 11
Cho hàm số \(y = {x^3} - 3{x^2} + 4x - 1\) có đồ thị là \((C)\). Hệ số góc nhỏ nhất của tiếp tuyến tại một điểm \(M\) trên đồ thị \((C)\) là
A. 1 .
B. 2.
C. -1 .
D. 3 .
\(y'=\left(x^3-3x^2+4x-1\right)'=3x^2-3\cdot2x+4\)
\(=3x^2-6x+3+1=3\left(x-1\right)^2+1>=1\)
Dấu = xảy ra khi x=1
=>Chọn A
Tiếp tuyến của đồ thị hàm số y = x 3 3 + 3 x 2 − 2 có hệ số góc k=9, có phương trình là:
A. y + 16 = − 9 x + 3
B. y − 16 = − 9 x − 3
C. y − 16 = − 9 x + 3
D. y = − 9 x + 3
Đáp án là C.
+ y ' = x 2 + 6 x = − 9 ⇔ x = − 3
+ Phương trình tiếp tuyến tại − 3 ; 16 là: y = − 9 x + 3 + 16.
Tiếp tuyến của đồ thị hàm số y = x 3 3 + 3 x 2 - 2 có hệ số góc k = - 9 có phương trình là:
A. y = -9x-11
B. A. y = -9x-27
C. y = -9x+43
D. y = -9x+11
- Tập xác định: D = R
- Đạo hàm: y ' = x 2 + 6 x .
- Tiếp tuyến có hệ số góc k = -9 nên:
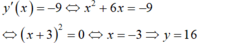
- Phương trình tiếp tuyến cần tìm là:
y = - 9(x + 3) + 16 hay y = -9x - 11
Chọn A.