Cho biết 3 cos α − sin α = 1 , 0 0 < α < 90 0 . Giá trị của tan α bằng
A. tan α = 4 3 .
B. tan α = 3 4 .
C. tan α = 4 5 .
D. tan α = 5 4 .
Cho góc α thỏa mãn 5 sin 2 α - 6 cos α = 0 và 0 < α < π 2 .
Tính giá trị của biểu thức: A = cos ( π 2 - α ) + sin ( 2015 π - α ) - c o t ( 2016 π + α ) .
A. - 2 15
B. 4 15
C. 1 15
D. - 3 5
Cho cos α = 3/4. Hãy tìm sin α , tg α , cotg α 0 ° < α < 90 °
Cho sin α = 1/2. Hãy tìm cos α , tg α , cotg α 0 ° < α < 90 °
Cho sinα=3/5 và 0<α<π/2. Khi đó, giá trị của A= sin(π−α)+cos(π+α)+cos(−α) là gì?
Online chờ gấp, đa tạ các vị!
`A=sin(π-α)+cos(π+α)+cos(-α)`
`= sinα-cosα+cosα=sinα=3/5`
Cho góc α thỏa mãn 0 < α < π 4 v à sin α + cos α = 5 2 . Giá trị của biểu thức P = sin α - cosα là:
A. P = 3 2
B. P = 1 2
C. P = - 1 2
D. P = - 3 2
Chọn D.
Xét biểu thức (sin α - cosα ) 2 + (sin α + cosα ) 2 ta có:
(sin α - cosα ) 2 + (sin α + cosα ) 2
= sin 2 α - 2sin α.cosα + cos 2 α + sin 2 α + 2 sin α.cosα + cos 2 α
= 2( sin 2 α + cos 2 α ) =2
⇒ (sin α - cosα ) 2 = 2 - (sin α + cosα ) 2
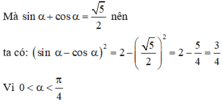
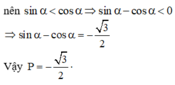
Cho góc nhọn α biết rằng cos α - sin α = 1/3 . Giá trị của sin α .cos α là
A. 2 3
B. 3 2
C. 4 9
D. 9 4
Cho biết 0≤α≤π20≤α≤π2 sao cho
sin3(α)+cos3(α)=1sin3(α)+cos3(α)=1
Và β=sin(α)+cos(α)β=sin(α)+cos(α)
a) Tính ∑α=07π2(sin−1(β)+α)∑α=07π2(sin−1(β)+α)
b) Chứng minh rằng số ββ thỏa đề bài là nghiệm của phương trình: β3−6β+5=0
Cho a ∈ ( 0 ; π 2 ] và thỏa mãn c o s α 2 sin 2 α + sin α - 3 = 0 . Tính giá trị của c o t α 2
A. y = sin2x
B. y = 2cosx + 3
C. y = sinx + cosx
D. y = tan2x + cotx
Cho a ∈ ( 0 ; π 2 ] và thỏa mãn c o s α 2 sin 2 α + sin α - 3 = 0 . Tính giá trị của c o t α 2
A. 1 2
B. 3 2
C. 4
D. 1
Cho góc α cho thỏa 0 < α < π 4 và sin α + cos α = 5 2 Tính P = sin α -cos α .
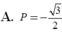
![]()
![]()
![]()