a) Xét ΔABD vuông tại A và ΔEBD vuông tại E có

BD chung

\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))

Do đó: ΔABD=ΔEBD(Cạnh huyền-góc nhọn)

b) Ta có: ΔABD=ΔEBD(cmt)

nên DA=DE(hai cạnh tương ứng)

Xét ΔDAE có DA=DE(cmt)

nên ΔDAE cân tại D(Định nghĩa tam giác cân)

c) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:

\(BC^2=AB^2+AC^2\)

\(\Leftrightarrow BC^2=8^2+6^2=100\)

hay BC=10(cm)

Chu vi tam giác ABC là:

\(C_{ABC}=AB+BC+AC=8+6+10=24\left(cm\right)\)

Câu 1:

a: \(A=15\sqrt{4a}+\sqrt{a}-\sqrt{25a}\)

\(=15\cdot2\sqrt{a}+\sqrt{a}-5\sqrt{a}\)

\(=30\sqrt{a}-4\sqrt{a}=26\sqrt{a}\)

b: Sửa đề: Khi a=100

Thay a=100 vào A, ta được:

\(A=26\cdot\sqrt{100}=26\cdot10=260\)

Gọi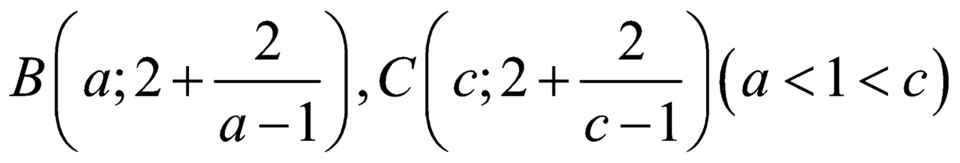  

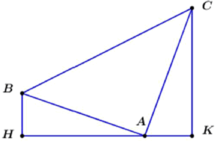
Gọi H, K lần lượt là hình chiếu của B, C trên trục  

vuông cân

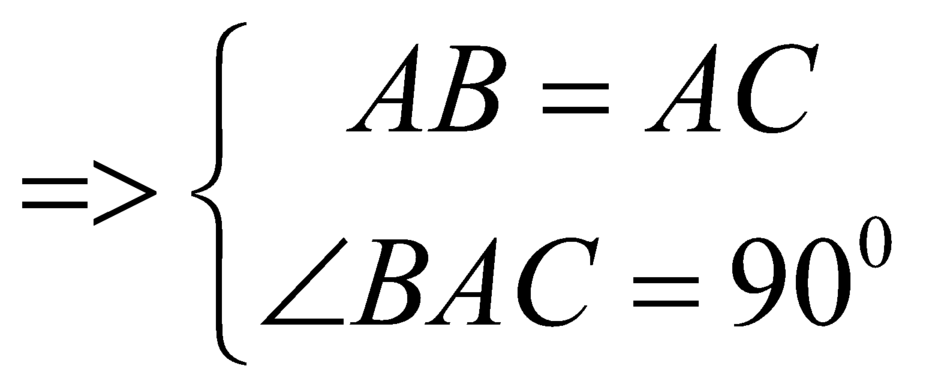
Ta có:

Mà: 

Xét và ta có:

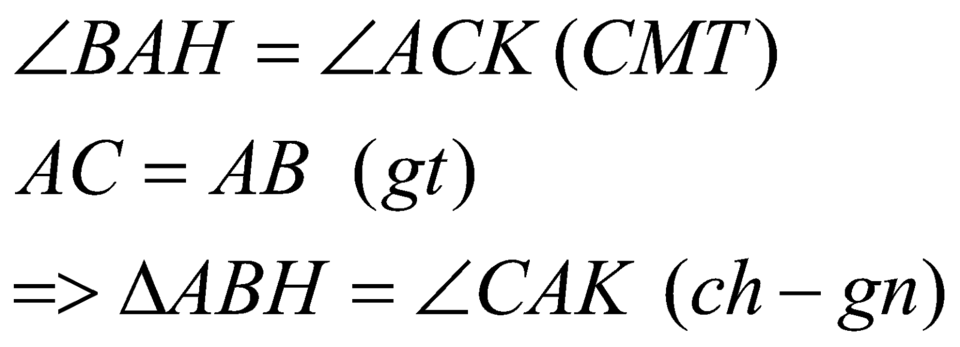
(các cạnh tương ứng bằng nhau)

Ta có: 

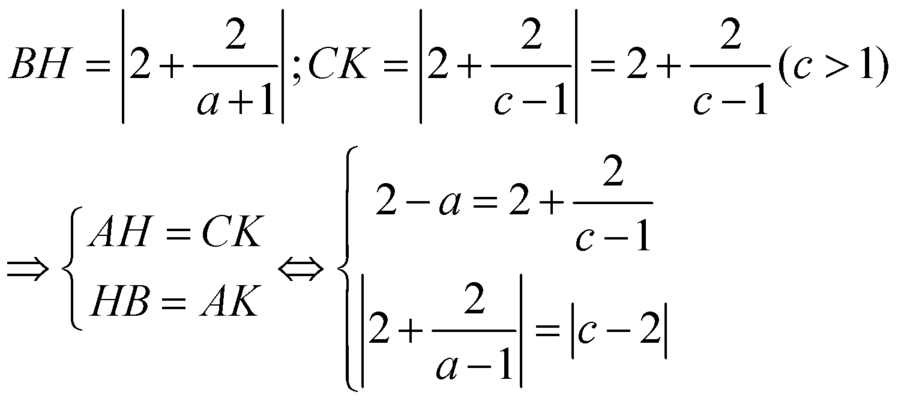
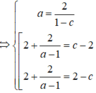
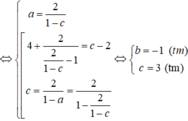
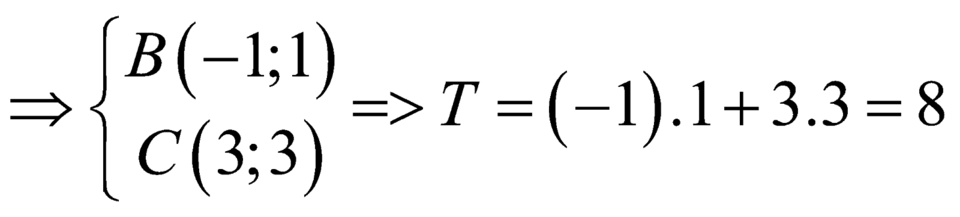
Chọn D.

3:

góc C=90-50=40 độ

Xét ΔABC vuông tại A có sin C=AB/BC

=>4/BC=sin40

=>\(BC\simeq6,22\left(cm\right)\)

\(AC=\sqrt{BC^2-AB^2}\simeq4,76\left(cm\right)\)

1:

góc C=90-60=30 độ

Xét ΔABC vuông tại A có

sin B=AC/BC

=>3/BC=sin60

=>\(BC=\dfrac{3}{sin60}=2\sqrt{3}\left(cm\right)\)

=>\(AB=\dfrac{2\sqrt{3}}{2}=\sqrt{3}\left(cm\right)\)

+)ΔABC vuông tại A \(\Rightarrow\widehat{A}=90^o\)

+)Áp dụng định lý tổng ba góc trong tam giác vào tam giác ABC, ta có:

\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)

\(=>90^o+40^o+\widehat{C}=180^o\)

\(=>\widehat{C}=180^o-90^o-40^o=50^o\)

Vậy \(\widehat{C}=50^o\)

------------------------------------------

+)Tam giác ABC vuông tại B \(\Rightarrow\widehat{B}=90^o\)

+)\(\widehat{A}=2.\widehat{C}\Rightarrow\widehat{A}+\widehat{C}=2.\widehat{C}+\widehat{C}=3.\widehat{C}\)

+)Áp dụng định lý tổng ba góc trong tam giác vào tam giác ABC, ta có:

\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)

\(\Rightarrow\widehat{A}+90^o+\widehat{C}=180^o\)

\(=>\widehat{A}+\widehat{C}=180^o-90^o\)

\(=>3.\widehat{C}=90^o\)

\(=>\widehat{C}=\dfrac{90^o}{3}=30^o\)

+)\(\widehat{A}=2.\widehat{C}\Rightarrow\widehat{A}=2.30^o=60^o\)

Vậy: \(\widehat{A}=60^o\) ; \(\widehat{C}=30^o\)

1: góc C=90-40=50 độ

2: góc A=2/3*90=60 độ

góc C=90-60=30 độ

a)

\(P \Rightarrow Q\): “Nếu tam giác ABC là tam giác vuông tại A thì các cạnh của nó thỏa mãn \(A{B^2} + A{C^2} = B{C^2}\)”

Mệnh đề này đúng.

\(Q \Rightarrow P\): “Nếu tam giác ABC có các cạnh thỏa mãn \(A{B^2} + A{C^2} = B{C^2}\) thì tam giác ABC vuông tại A”

Mệnh đề này đúng.

\(P \Leftrightarrow Q\): “Tam giác ABC là tam giác vuông tại A khi và chỉ khi các cạnh của nó thỏa mãn \(A{B^2} + A{C^2} = B{C^2}\)”

Mệnh đề này đúng do các mệnh đề \(P \Rightarrow Q,Q \Rightarrow P\)đều đúng.

\(\overline P  \Rightarrow \overline Q \): “Nếu tam giác ABC không là tam giác vuông tại A thì các cạnh của nó thỏa mãn \(A{B^2} + A{C^2} \ne B{C^2}\)”

Mệnh đề này đúng.

b) Mệnh đề \(P \Rightarrow Q\) có thể phát biểu là:

“Tam giác ABC là tam giác vuông tại A là điều kiện đủ để tam giác ABC có các cạnh thỏa mãn \(A{B^2} + A{C^2} = B{C^2}\)”

“Tam giác ABC có các cạnh thỏa mãn \(A{B^2} + A{C^2} = B{C^2}\) là điều kiện cần để tam giác ABC vuông tại A”

c)

X là tập hợp các tam giác ABC vuông tại A.

 Y là tập hợp các tam giác ABC có trung tuyến \(AM = \frac{1}{2}BC\).

Dễ thấy: \(X \subset Y\) do các tam giác ABC vuông thì đều có trung tuyến \(AM = \frac{1}{2}BC\).

Ta chứng minh: Nếu tam giác ABC có trung tuyến \(AM = \frac{1}{2}BC\) thì tam giác ABC vuông tại A.

Thật vậy, \(BM = MC = AM = \frac{1}{2}BC\) suy ra M là tâm đường tròn đường kính BC, ngoại tiếp tam giác ABC.

\( \Rightarrow \widehat {BAC} = {90^ \circ }\) (góc nội tiếp chắn nửa đường tròn)

Vậy tam giác ABC là tam giác vuông.

Do đó \(Y \subset X\)

Vậy \(X = Y\)