Cho S = ∫ 0 π 2 2 x - 1 - sin x d x .Biết I = π 2 a - π b - 1 Cho
các mệnh đề sau:(1) a = 2b
(2) a + b = 5
(3) a +3b = 10
(4) 2a + b = 10
Các phát biểu đúng
A. (1),(2),(3)
B. (2),(3),(4)
C. (1),(2),(4)
D. (1),(3),(4)
Trong các cặp hình phẳng giới hạn bởi các đường sau, cặp nào có diện tích bằng nhau?
a) {y = x + sinx, y = x với 0 ≤ x ≤ π } và {y = x + sinx, y = x với π ≤ x ≤ 2 π }
b) {y = sinx, y = 0 với 0 ≤ x ≤ π } và {y = cosx, y = 0 với 0 ≤ x ≤ π };
c) {y = x , y = x 2 }
và { y = 1 - x 2 , y = 1 − x}
Cho hàm số f(x)=3 sinx+2. Gọi S là tập hợp các giá trị nguyên của tham số m để hàm số y = f 3 ( x ) - 3 mf 2 ( x ) + 3 ( m 2 - 4 ) f ( x ) - m nghịch biến trên khoảng (0;π/2). Số tập con của S bằng
A. 1
B. 2.
C. 4.
D. 16.
Cho hàm số f(x) có đạo hàm liên tục trên đoạn 0 ; π thỏa mãn: ∫ 0 π f ' x d x = ∫ 0 π cos x . f x d x = π / 2 và f π / 2 = 1 . Khi đó tích phân ∫ 0 π / 2 f x d x bằng
A.0.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số f(x) = sin3x.
Tính f''(-π/2), f''(0), f''(π/18)
f''(-π/2) = -9, f''(0) = 0, f''(π/18) = -9/2
Cho hàm số
f x = x + 1 ; x < - π 2 sin x x ; - π < x < 0 x + 2 ; x ≥ 0
Mệnh đề nào sau đây là đúng?
A. Hàm số gián đoạn tại điểm x = - π
B. Hàm số gián đoạn tại các điểm x = 0; x = - π
C. Hàm số gián đoạn tại điểm x = 0
D. Hàm số không có điểm gián đoạn.
Tại điểm x = - π hàm số không xác định nên hàm số gián đoạn.
Ta có
lim x → 0 - f x = lim x → 0 - 2 sin x x = 2 lim x → 0 + f x = lim x → 0 + x + 2 = 2 = f 0
Do lim x → 0 + f(x) = lim x → 0 - f(x) = f(0) nên hàm số liên tục tại điểm x = 0.
Vậy hàm số chỉ gián đoạn tại điểm x = - π
Đáp án A
Tìm nghiệm của các phương trình sau trong khoảng đã cho
a) sin2x = -\(\frac{1}{2}\) với 0<x<π ;
b) cos(x-5) = \(\frac{\sqrt{3}}{2}\) với -π< x < π.
Cho x ϵ (0;π/2). Biết log(sinx)+log(cosx)=-1 và log(sinx+cosx)=1/2(logn-1). Giá trị của n là
A. 11.
B. 12.
C. 10.
D. 15.
Trong các khoảng sau, m thuộc khoảng nào để phương trình sin^2 x-(2m+1) sin x.cos x + 2m cos^2 x = 0 có nghiệm thuộc khoảng (π/4 ; π/3)?
\(sin^2x-2m.sinx.cosx-sinx.cosx+2mcos^2x=0\)
\(\Leftrightarrow sinx\left(sinx-cosx\right)-2mcosx\left(sinx-cosx\right)=0\)
\(\Leftrightarrow\left(sinx-cosx\right)\left(sinx-2m.cosx\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}sinx=cosx\\sinx=2m.cosx\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}tanx=1\\tanx=2m\end{matrix}\right.\)
Do \(tanx=1\) ko có nghiệm đã cho nên \(tanx=2m\) phải có nghiệm trên khoảng đã cho
\(\Rightarrow tan\left(\dfrac{\pi}{4}\right)< 2m< tan\left(\dfrac{\pi}{3}\right)\)
\(\Rightarrow1< 2m< \sqrt[]{3}\)
\(\Rightarrow m\in\left(\dfrac{1}{2};\dfrac{\sqrt{3}}{2}\right)\) (hoặc có thể 1 đáp án là tập con của tập này cũng được)
Cho f(x)= log 5 ( sin x ) , x ∈ ( 0 ; π / 2 ) . Tính f'(x)
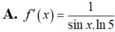
![]()
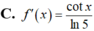
![]()
Cho sinα = 8/17, sinβ = 15/17 với 0 < α < π/2, 0 < β <π/2. Chứng minh rằng: α + β = π/2