Giải và biện luận theo tham số m hệ phương trình:
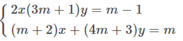
Cho hệ phương trình \(|^{mx+2y=1}_{3x+\left(m+1\right)y=-1}\) (với m là tham số)
a) Giải hệ phương trình với m = 3.
b) Giải và biện luận hệ phương trình theo m.
c) Tìm m để hệ phương trình có nghiệm là số nguyên.
Cho hệ phương trình (m là tham số): 2mx+y=2 8x+my=m+2 Giải và biện luận hệ phương trình đã cho theo m Mn giúp em với ạ
2mx+y=2 và 8x+my=m+2
=>y=2-2mx và 8x+m(2-2mx)=m+2
=>\(\left\{{}\begin{matrix}8x+2m-2m^2x-m-2=0\\y=-2mx+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\left(-2m^2+8\right)=-m+2\\y=-2mx+2\end{matrix}\right.\)
=>2(m-2)(m+2)x=m-2 và y=-2mx+2
Nếu m=2 thì hệpt có vô số nghiệm
Nếu m=-2 thìhệ pt vn
Nếu m<>2; m<>-2 thì hệ phương trình có nghiệm duy nhất là:
\(\left\{{}\begin{matrix}x=\dfrac{1}{2\left(m+2\right)}\\y=-2m\cdot\dfrac{1}{2\left(m+2\right)}+2=-\dfrac{m}{m+2}+2=\dfrac{-m+2m+4}{m+2}=\dfrac{m+4}{m+2}\end{matrix}\right.\)
Giải giúp em với ạ:
Cho hệ phương trình: mx + 4y = 10 - m và x + my = 4 (m là tham số)
a, giải hệ phương trình khi m = √2
b, giải và biện luận hệ phương trình theo m
Cô làm câu b thôi nhé :)
Ta có hệ \(\hept{\begin{cases}mx+4y=10-m\\x+my=4\end{cases}}\Leftrightarrow\hept{\begin{cases}m\left(4-my\right)+4y=10-m\\x=4-my\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(4-m^2\right)y=10-5m\left(1\right)\\x=4-my\end{cases}}\)
Với \(4-m^2=0\Leftrightarrow m=2\) hoặc \(m=-2\)
Xét m =2, phương trình (1) tương đương 0.x = 0. Vậy hệ phương trình có vô số nghiệm dạng \(\left(4-2t;t\right)\)
Xét m = -2, phương trình (1) tương đương 0.x = 20. Vậy hệ phương trình vô nghiệm.
Với \(4-m^2\ne0\Leftrightarrow m\ne2\) và \(m\ne-2\), phương trình (1) tương đương \(y=\frac{10-5m}{4-m^2}=\frac{5}{2+m}\)
Từ đó : \(x=\frac{8-m}{2+m}\)
Kết luận:
+ m = 2, hệ phương trình có vô số nghiệm dạng \(\left(4-2t;t\right)\)
+ m = - 2, hệ phương trình vô nghiệm.
+ \(m\ne2;m\ne-2\) hệ có 1 nghiệm duy nhất \(\hept{\begin{cases}x=\frac{8-m}{2+m}\\y=\frac{5}{2+m}\end{cases}}\)
Chúc em học tập tốt :)

hehe
Hỏi từ lâu nhưng bây giờ em trả lời lại cho vui
giải và biện luận hệ phương trình theo tham số m:
{mx-y=2m và 4x-my=6+m
.cho phương trình ẩn x:ax2+(b-m)x+c=0 .Viết chương trình :
a) giải phương trình với hệ số a=0.
b)biện luận nghiệm của phương trình theo tham số m.
Giải và biện luận theo tham số m các phương trình sau:
![]()
Điều kiện của phương trình là x ≠ -1, ta có
![]()
⇒ (m - 2)x + 3 = (2m - 1)(x + 1)
⇒ (m + 1)x = 4 - 2m (1)
Với m = -1 phương trình (1) vô nghiệm nên phương trình đã cho cũng vô nghiệm.
Với m ≠ -1 phương tình (1) có nghiệm ![]()
Nghiệm này thỏa mãn điều kiện x ≠ -1 khi và chỉ khi 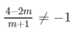 hay -2m + 4 ≠ -m - 1 ⇒ m ≠ 5
hay -2m + 4 ≠ -m - 1 ⇒ m ≠ 5
Kết luận
Với m = -1 hoặc m = 5 phương trình vô nghiệm
Với m ≠ -1 và m ≠ 5 phương trình có nghiệm là ![]()
Giải và biện luận các phương trình sau theo tham số m.
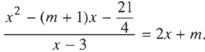
Điều kiện của phương trình là: x ≠ 3. Ta có:
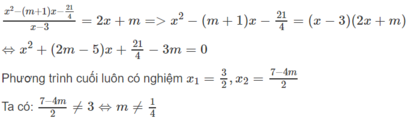
Kết luận
Với m ≠ 1/4 phương trình đã cho có hai nghiệm và x = 3/2 và x = (7 - 4m)/2
Với m ≠ 1/4 phương trình có một nghiệm x = 3/2
Giải và biện luận các phương trình sau theo tham số m.
![]()
Với m = -1 phương trình đã cho trở thành
-5x + 1 = 0 ⇔ x = 1/5
Với m ≠ -1 phương trình đã cho là một phương trình bậc hai, có biệt thức Δ = -24m + 1
Nếu m ≤ 1/24 thì Δ ≥ 0 phương trình có hai nghiệm

Với m = -1 phương trình có nghiệm là x = 1/5
Giải và biện luận theo tham số m các phương trình sau:
![]()
Điều kiện của phương trình là x ≠ 1. Khi đó ta có
![]()
⇔ (2m + 1)x - m = (x + m)(x - 1)
⇔ x2 - (m + 2)x = 0
⇔ x = 0, x = m + 2
Giá trị x = m + 2 thỏa mãn điều kiện của phương trình khi m ≠ -1
Kết luận
Vậy với m = -1 phương trình có nghiệm duy nhất x = 0;
Với m ≠ -1 phương trình có hai nghiệm x = 0 và x = m + 2.