Hai đường thẳng (a) 4x+ 3y- 18= 0 và (b) : 3x+ 5y-19= 0 cắt nhau tại điểm có toạ độ:
A.(2; -3)
B. (3; 2)
C.(1; 3)
D.(2;4)
Trong mặt phẳng tọa độ Oxy, hai đường thẳng d 1 : 4 x + 3 y - 18 = 0 ; d 2 : 3 x + 5 y - 19 = 0 cắt nhau tại điểm có toạ độ là
![]()
![]()
![]()
![]()
Trong mặt phẳng tọa độ Oxy, hai đường thẳng d 1 : 4 x + 3 y - 18 = 0 ; d 2 = 3 x + 5 x - 19 = 0 cắt nhau tại điểm có toạ độ là
A. A 3 ; - 2
B. B - 3 ; 2
C. C 3 ; 2
D. D - 3 ; - 2
Cho đường tròn C x^2 + y² + 2x + 5y - 15 = 0 Viết phương trình đường thẳng vuông góc với đường thẳng delta: 4x + 3y - 2 = 0 cắt đường tròn C tại hai điểm a và b sao cho ab=6
Cho đường tròn C x^2 + y² + 2x + 5y - 15 = 0 Viết phương trình đường thẳng vuông góc với đường thẳng delta: 4x + 3y - 2 = 0 cắt đường tròn C tại hai điểm a và b sao cho ab=6 Giúp với mọi người ơiii SOS
Sửa đề: x^2+y^2+2x+6y-15=0
Δ vuông góc d nên Δ: 3x+4y+c=0
(C);x^2+y^2+2x+6y-15=0
=>x^2+2x+1+y^2+6y+9-25=0
=>(x+1)^2+(y+3)^2=25
=>R=5; I(-1;-3)
Kẻ IH vuông góc AB
=>H là trung điểm của AB
=>AH=6/2=3cm
=>IH=4cm
=>d(I;Δ)=IH=4
=>|c+3-12|/5=4
=>c=-11 hoặc c=29
=>3x+4y-11=0 hoặc 3x+4y+29=0
Trong mặt phẳng toạ độ Oxy cho hai đường thẳng d1 : x + y − 1 = 0; d2 : 3x − y + 5 = 0 cắt
nhau tại A. Viết phương trình đường thẳng ∆ đi qua điểm M(2; 2) và cắt d1, d2 lần lượt tại B, C thoả
mãn AB = BC.
Tọa độ A là nghiệm: \(\left\{{}\begin{matrix}x+y-1=0\\3x-y+5=0\end{matrix}\right.\) \(\Rightarrow A\left(-1;2\right)\)
Gọi \(\alpha\) là góc giữa d1 và d2 \(\Rightarrow cos\alpha=\frac{\left|3-1\right|}{\sqrt{2}.\sqrt{10}}=\frac{\sqrt{5}}{5}\)
Do \(AB=BC\Rightarrow\Delta ABC\) cân tại B
Gọi \(\beta\) là góc giữa \(\Delta\) và \(d_1\) \(\Rightarrow\alpha=\beta\)
Giả sử \(\Delta\) nhận \(\left(a;b\right)\) là vtpt
\(\Rightarrow\frac{\left|a+b\right|}{\sqrt{2}\sqrt{a^2+b^2}}=\frac{\sqrt{5}}{5}\)
\(\Leftrightarrow5\left(a+b\right)^2=2\left(a^2+b^2\right)\)
\(\Leftrightarrow3a^2+10ab+3b^2=0\Rightarrow\left[{}\begin{matrix}3a=-b\\a=-3b\end{matrix}\right.\)
\(\Rightarrow\Delta\) có 2 vtpt là \(\left(1;-3\right);\left(3;-1\right)\)
Có 2 pt đường thẳng thỏa mãn:
\(\left[{}\begin{matrix}1\left(x-2\right)-3\left(y-2\right)=0\\3\left(x-2\right)-1\left(y-2\right)=0\end{matrix}\right.\)
Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn C : x + 1 2 + y - 2 2 = 9 và điểm I - 3 ; 3 . Đường thẳng ∆ : a x + b + c = 0 đi qua điểm I và cắt đường tròn (C) tại hai điểm A và B. Tiếp tuyến của A và B cắt nhau tại M. Biết điểm M thuộc đường thẳng x + 3 y - 4 = 0 . Tính P = 2 a + 3 b c
A. P = 1 3
B. P = - 11 4
C. P = 2 3
D. P = 1 4
Đáp án A.
Đường tròn (C) có tâm K(-1;2) và bán kính R = 3


Vậy phương trình đường thẳng D là
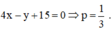
Cho đường thẳng ∆ : 3x-4y-19=0 và đường tròn C : x - 1 2 + y - 1 2 = 25 . Biết đường thẳng ∆ cắt (C) tại hai điểm phân biệt A và B, khi đó độ dài đoạn thẳng AB là
A. 6
B. 3
C. 4
D. 8
Trong một mặt phẳng toạ độ xOy cho tam giác AC vuông tại A có đường cao AH: x- 3y-16=0 cắt đường phân giác BD tại K( \(D\in AC\)) , đường thẳng đi qua K song song với AC và cắt cạnh huyền BC tại E ( 3;-7), biết điểm D thuộc đường thẳng\(\Delta:x-y-12=0\) và xA>3. Viết phương trình các cạnh của tam giác ABC
Hướng dẫn, hơi dài nên làm biếng giải chi tiết:
Kéo dài KE cắt AB tại F
BK là phân giác góc B nên hai tam giác vuông BKH và BKF bằng nhau (ch-gn)
\(\Rightarrow\widehat{BKF}=\widehat{BKE}\) \(\Rightarrow\widehat{BKA}=\widehat{BKE}\)
\(\Rightarrow\Delta BKA=\Delta BKE\left(g.c.g\right)\)
\(\Rightarrow AK=EK\)
Lại có \(\widehat{BKF}=\widehat{BDA}\) (đồng vị) \(\Rightarrow\widehat{BDA}=\widehat{BKH}=\widehat{AKD}\)
\(\Rightarrow\Delta AKD\) cân tại A hay \(AK=AD\)
\(\Rightarrow AD=EK\Rightarrow ADEK\) là hình bình hành hay DE song song AK (hay AH)
BC vuông góc AH nên nhận (3;1) là 1 vtpt và đi qua E(3;-7) \(\Rightarrow\) pt BC
ED đi qua E(3;-7) và song song AH nên nhận (1;-3) là 1 vtpt \(\Rightarrow\) pt DE
\(\Rightarrow\) Tọa độ D (giao của DE và \(\Delta\))
ADEK là hbh (theo cmt) và có 2 cạnh kề AK=AD nên ADEK là hình thoi
\(\Rightarrow AD=DE\)
Biết tọa độ D, E \(\Rightarrow\) độ dài DE
A thuộc AH nên tọa độ A có dạng: \(A\left(3a+16;a\right)\Rightarrow\overrightarrow{DA}=...\Rightarrow\left|\overrightarrow{DA}\right|=DE\)
\(\Rightarrow a\Rightarrow\) tọa độ A
\(\Rightarrow\) Phương trình AC (qua A và D)
\(\Rightarrow\) Phương trình AB (qua A và vuông góc AC)
cho hàm số y=mx+n-3x (d).Xác định m,n để đường thẳng (d)
a, đi qua điểm A(1,-3);B(-2,3)
b,Cắt trục tung tại điểm có tung độ bằng 1-√3,cắt trục hoành tại điểm có hoành độ bằng 3+√3
c,cắt đường thẳng 3y-x-4=0
d,song song với đường thẳng 2x+5y=-1
d: Để (d)//\(y=\dfrac{-2x-1}{5}=\dfrac{-2}{5}x-\dfrac{1}{5}\) thì
\(\left\{{}\begin{matrix}m-3=\dfrac{-2}{5}\\n\ne-\dfrac{1}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{13}{5}\\n\ne-\dfrac{1}{5}\end{matrix}\right.\)