Tìm m để đường thẳng (d): y = x + 3 ; ( d ’ ) : y = − x + 1 ; ( d ’ ’ ) : y = 3 x – m – 2 đồng quy
A. m = 4 + 3
B. m = − 4 − 3
C. m = 4 − 3
D. m = 2 + 3
Cho đường thẳng (d): y = (m + 3)x + 4 (m là tham số, m -3)
a) Tìm m để đường (d) song song với đường thẳng y = 4x + 3
b) Vẽ đường thẳng (d) ứng với m tìm được ở trên.
c) Tìm tọa độ giao điểm của (d) với đường thẳng y = x - 1
a: Để hai đường song thì m+3=4
=>m=1
c: (d): y=4x+4
Tọa độ giao điểm là:
4x+4=x-1 và y=x-1
=>3x=-5 và y=x-1
=>x=-5/3 và y=-8/3
a) Tìm m, n để đường thẳng y = (2m -1)x + n (d) đi qua điểm A(2; -1) và B(1;4)
b) Tìm m để đường thẳng y = (m![]() + 3)x + m (d) song song với đường thẳng y = 4x-1(d’)
+ 3)x + m (d) song song với đường thẳng y = 4x-1(d’)
b: Để (d)//(d') thì m+3=4
hay m=1
Cho đường thẳng (d)y=(3-m)x+2
a) tìm m để (d) song song với đường thẳng y=x-1
b) vẽ đường thẳng d với m=0
a) Để (d) song song với đường thẳng y = x - 1.
=> 3 - m = 1.
<=> m = 2.
Cho hàm số : y = ( 3m-1)x +m ( m là tham số ) có đồ thị là đường thẳng (d)
a) tìm m để đường thẳng (d) cắt đường thẳng y = 5x - 3
b) Tìm m để đường thẳng ( d ) song song với đường thẳng : y = -4x + 1
1. Cho đường thẳng (d):y=2mx+2m-3 và Parabol (P):y=x\(^2\)
a) Tìm m để đường thẳng (d) đi qua A(1;5)
b) Tìm m để đường thẳng (d) tiếp xúc với Parabol (P)
a: Thay x=1 và y=5 vào (d), ta được:
2m+2m-3=5
=>4m-3=5
hay m=2
b: Phương trình hoành độ giao điểm là:
\(x^2-2mx-2m+3=0\)
Để(P) tiếp xúc với (d) thì \(\left(-2m\right)^2-4\left(-2m+3\right)=0\)
\(\Leftrightarrow4m^2+8m-12=0\)
\(\Leftrightarrow\left(m+3\right)\left(m-1\right)=0\)
=>m=-3 hoặc m=1
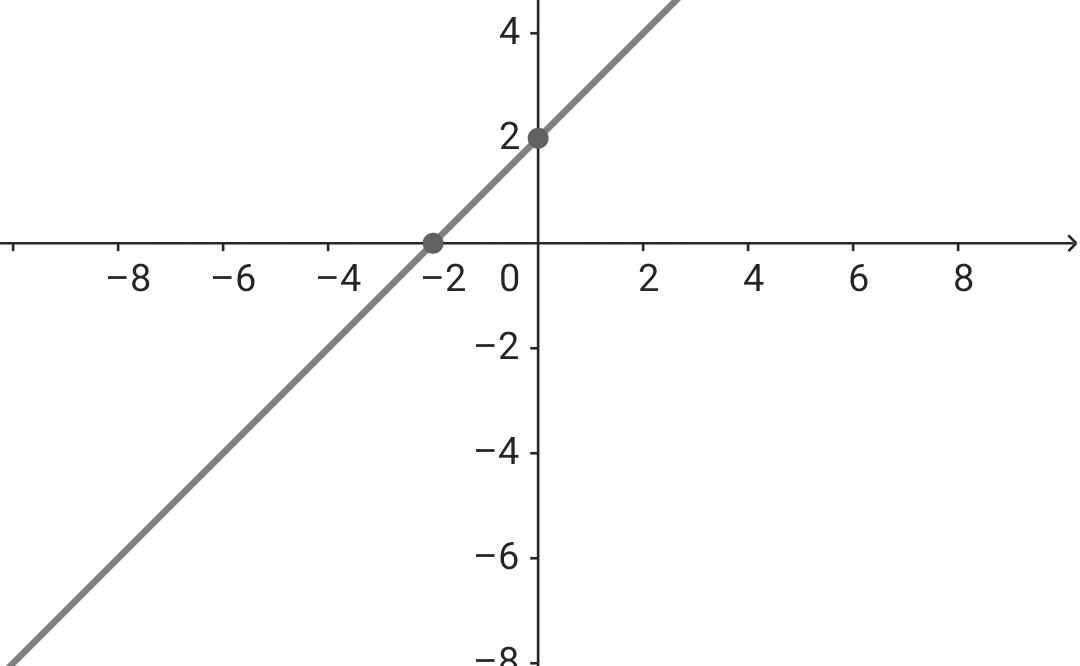
1/ Cho hàm số y=(m-3).x+2 (với x là biến số , m≠3) có đồ thị là đường thẳng (d) trong mặt phẳng tọa độ Oxy
a) Tìm các giá trị của m để đường thẳng (d) song song với đường thẳng (d'):y=x-5
b) Vẽ đường thẳng (d) với giá trị m vừa tìm được.
a) (d) // (d') khi m - 3 = 1
m = 1 + 3
m = 4
Vậy m = 4 thì (d) // (d')
b) Với m = 4 ⇒ (d): y = x + 2
Đồ thị:
cho đường thẳng d y = (m + 2) x + m Tìm m để d
a, song song với đường thẳng d1 : y = -2 x + 3
b ,vuông góc với đường thẳng d2 : y = 1 / 3 x + 1
C, đi qua điểm N( 1,3)
D, Tìm điểm cố định Mà D luôn đi qua với mọi m
\(a,d//d_1\Leftrightarrow\left\{{}\begin{matrix}m+2=-2\\m\ne3\end{matrix}\right.\Leftrightarrow m=-4\\ b,d\perp d_2\Leftrightarrow\dfrac{1}{3}\left(m+2\right)=-1\Leftrightarrow m+2=-3\Leftrightarrow m=-5\\ c,d.qua.N\left(1;3\right)\Leftrightarrow x=1;y=3\Leftrightarrow3=m+2+m\\ \Leftrightarrow2m=1\Leftrightarrow m=\dfrac{1}{2}\)
\(d,\) Gọi điểm đó là \(A\left(x_1;y_1\right)\)
\(\Leftrightarrow y_1=\left(m+2\right)x_1+m\\ \Leftrightarrow y_1-mx_1-2x_1-m=0\\ \Leftrightarrow-m\left(x_1+1\right)+y_1-2x_1=0\\ \Leftrightarrow\left\{{}\begin{matrix}x_1+1=0\\y_1-2x_1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=-1\\y_1=-2\end{matrix}\right.\)
Vậy \(A\left(-1;-2\right)\) luôn đi qua D với mọi m
cho đường thẳng (d):y=(m+2)x-m^2(m là tham số).tìm m để đường thẳng (d) và các đường thẳng y=x-1;x=2y=3 cắt nhau tại 1 điểm
Sửa đề: x+2y=3
Tọa độ giao là:
x-y=1 và x+2y=3
=>x=5/3 và y=2/3
Thay x=5/3 và y=2/3 vào (d), ta được"
5/3(m+2)-m^2=2/3
=>5/3m+10/3-m^2-2/3=0
=>-m^2+5/3m+8/3=0
=>-3m^2+5m+8=0
=>-3m^2+8m-3m+8=0
=>(3m-8)(-m-1)=0
=>m=-1 hoặc m=8/3
Cho đường thẳng (d): y=(m+2)x-m2 (m là tham số) .Tìm m để đường thẳng (d) và các đường thẳng y=x-1 ; x-2y=3 cắt nhau tại 1 điểm.
Ta có: y=x-1
nên x-1=y
=>x-y=1
Tọa độ giao điểm của hai đường x-y=1 và x-2y=3 là:
\(\left\{{}\begin{matrix}x-y=1\\x-2y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=-2\end{matrix}\right.\)
Thay x=-1 và y=-2 vào y=(m+2)x-m2, ta được:
\(-m^2+\left(-1\right)\cdot\left(m+2\right)=-2\)
\(\Leftrightarrow-m^2-m-2=-2\)
\(\Leftrightarrow m^2+m=0\)
=>m=0 hoặc m=-1
`x-2y=3<=>y=1/2x-3/2`
Xét hệ ptr:`{(y=x-1),(y=1/2x-3/2):}`
`<=>{(1/2x+1/2=0<=>x=-1),(y=-1-1=-2):}`
Để `(d)` cắt các đường thẳng `y=x-1` và `x-2y=3` tại `1` điểm thì `3` đường thẳng này phải đồng quy
Tức là: `x=-1;y=-2` thuộc `(d)`
`=>-2=(m+2).(-1)-m^2`
`<=>m^2+m=0`
`<=>m(m+1)=0`
`<=>m=0` hoặc `m=-1`
Vậy `m={0;-1}`
Cho hàm số y = (m+1)x − 2m+1 (d)
a) Xác định m để đường thẳng (d) đi qua gốc tọa độ.
b) Tìm m để đường thẳng (d) đi qua A(3; 4).Vẽ đồ thị với m vừa tìm được.
c) Tìm tọa độ giao điểm của đường thẳng vừa vẽ với đường thẳng (d’): y = −2x + 4
\(a,\Leftrightarrow A\left(0;0\right)\in\left(d\right)\Leftrightarrow-2m+1=0\Leftrightarrow m=\dfrac{1}{2}\\ b,\Leftrightarrow x=3;y=4\Leftrightarrow3\left(m+1\right)-2m+1=4\\ \Leftrightarrow3m+3-2m+1=4\\ \Leftrightarrow m=0\Leftrightarrow\left(d\right):y=x+1\\ c,\text{PT hoành độ giao điểm: }x+1=-2x+4\Leftrightarrow x=1\Leftrightarrow y=2\Leftrightarrow B\left(1;2\right)\\ \text{Vậy }B\left(1;2\right)\text{ là giao 2 đths}\)