Trong mặt phẳng tọa độ; cho ba vectơ a → 1 ; 2 ; b → 4 ; 3 ; c → 2 ; 3 . Tính P = a → b → + c →
A. 0
B. 18
C. 20
D. 28
Trong mặt phẳng tọa độ Oxyz, cho phương trình tổng quát của mặt phẳng (P): 2x - 6y - 8z+ 1 = 0. Một véc tơ pháp tuyến của mặt phẳng ( P) có tọa độ là
A. (-1;3;4)
B. (1;3;4)
C. (1;-3;-4)
D. (1;-3;4)
Trong không gian với hệ tọa độ Oxyz, cho điểm M(3;2;1). Mặt phẳng (P) đi qua điểm M và cắt các trục tọa độ Ox, Oy, Oz lần lượt tại các điểm A, B, C không trùng với điểm gốc tọa độ sao cho M là trực tâm tam giác ABC. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (P).
A. 3 x + 2 y + z + 14 = 0
B. 2 x + y + 3 z + 9 = 0
C. 3 x + 2 y + z - 14 = 0
D. 2 x + y + z - 9 = 0
Đáp án A.
Ta có A M ⊥ B C ⊥ O A ⇒ B C ⊥ O A M ⇒ B C ⊥ O M
Tương tự ta cũng có O M ⊥ A C ⇒ O M ⊥ P ⇒ P (P) nhận O M ¯ = 3 ; 2 ; 1 là vecto pháp tuyến.
Trong các đáp án, chọn đáp án mặt phẳng có vecto pháp tuyến có cùng giá với O M ¯ và không chứa điểm M thì thỏa.
Trong không gian với hệ tọa độ Oxyz, cho điểm M(3;2;1). Mặt phẳng (P) đi qua M và cắt các trục tọa độ Ox, Oy, Oz lần lượt tại các điểm A, B, C không trùng với gốc tọa độ sao cho M là trực tâm tam giác ABC. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (P).
A. 3x+2y+z+14=0
B. 2x+y+3z+9=0
C. 3x+2y+z-14=0
D. 2x+y+z-9=0.
Chọn A
Gọi A(a;0;0);B(0;b;0);C(0;0;c)
Phương trình mặt phẳng (P) có dạng:
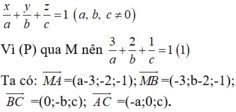
Vì M là trực tâm của tam giác ABC nên:
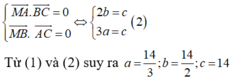
Khi đó phương trình (P): 3x+2y+z-14=0.
Vậy mặt phẳng song song với (P) là: 3x+2y+z+14=0.
(1) trong mặt phẳng tọa độ Oxy, cho hai vecto \(\overrightarrow{a}=\left(1;-4\right)\), \(\overrightarrow{b}=\left(0;2\right)\). tọa độ của vecto \(\overrightarrow{u}=2\overrightarrow{a}-\overrightarrow{b}\) là?
(2) trong mặt phẳng tọa độ Oxy, cho hai vecto \(\overrightarrow{a}=\left(-7;3\right)\), \(\overrightarrow{b}=\left(4;1\right)\). tọa độ của vecto \(\overrightarrow{u}=\overrightarrow{b}-2\overrightarrow{a}\) là?
(3) trong mặt phẳng tọa độ Oxy, cho hai vecto \(\overrightarrow{u}=\left(-5;4\right)\), \(\overrightarrow{v}=-3\overrightarrow{j}\). tọa độ của vecto \(\overrightarrow{a}=2\overrightarrow{u}-5\overrightarrow{v}\) là?
(4) trong mặt phẳng tọa độ Oxy, cho hai điểm A (1;1), B (4;-7) và \(\overrightarrow{OM}=2\overrightarrow{OA}-5\overrightarrow{OB}\). tổng hoành độ và tung độ của điểm M là?
giúp mk vs ạ mk cần gấp thank
(1); vecto u=2*vecto a-vecto b
=>\(\left\{{}\begin{matrix}x=2\cdot1-0=2\\y=2\cdot\left(-4\right)-2=-10\end{matrix}\right.\)
(2): vecto u=-2*vecto a+vecto b
=>\(\left\{{}\begin{matrix}x=-2\cdot\left(-7\right)+4=18\\y=-2\cdot3+1=-5\end{matrix}\right.\)
(3): vecto a=2*vecto u-5*vecto v
\(\Leftrightarrow\left\{{}\begin{matrix}a=2\cdot\left(-5\right)-5\cdot0=-10\\b=2\cdot4-5\cdot\left(-3\right)=15+8=23\end{matrix}\right.\)
(4): vecto OM=(x;y)
2 vecto OA-5 vecto OB=(-18;37)
=>x=-18; y=37
=>x+y=19
Trong hệ trục tọa độ , cho mặt phẳng (P) có phương trình 3 x - z + 1 = 0 . Véctơ pháp tuyến của mặt phẳng (P) có tọa độ là
A. (3;0;-1)
B. (3;-1;1)
C. (3;-1;0)
D. (-3;1;1)
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng: 5 x − 2 y − 3 x + 7 = 0 . Tìm tọa độ vectơ pháp tuyến n → của mặt phẳng.
A. n → = − 5 ; 2 ; − 3 .
B. n → = − 5 ; − 2 ; − 3 .
C. n → = − 5 ; 2 ; 3 .
D. n → = 5 ; 2 ; 3 .
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : 2 x - z + 1 = 0 . Tọa độ một véctơ pháp tuyến của mặt phẳng (P) là:
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : 2 x − z + 1 = 0. Tọa độ một
véctơ pháp tuyến của mặt phẳng P là
A. n → = 2 ; − 1 ; 1
B. n → = 2 ; 0 ; 1
C. n → = 2 ; 0 ; − 1
D. n → = 2 ; − 1 ; 0
Trong hệ trục tọa độ Oxyz, cho mặt phẳng (P) có phương trình 3x - z + 1 = 0 Véctơ pháp tuyến của mặt phẳng (P) có tọa độ là
A. (3;0; - 1)
B. (3; - 1;1)
C. (3; - 1;0)
D. ( - 3;1;1)
Trong hệ trục tọa độ Oxyz, cho mặt phẳng (P) có phương trình 3x-z+1=0. Véctơ pháp tuyến của mặt phẳng (P) có tọa độ là
A. (3;0;-1)
B. (3;-1;1)
C. (3;-1;0)
D. (-3;1;1)