Với a, b là các số thực dương bất kì, đẳng thức nào sau đây sai?
A. a α a β = a α - β
B. a α . a β = a α + β
C. a α a β = a b α - β
D. a α . b α = a b α
Cho số dương a khác 1 và các số thực α ; β . Đẳng thức nào sau đây là sai?
A. a α . a β = a α . β
B. a α . a β = a α + β
C. a α β = a α . β
D. a α a β = a α - β
Cho số dương a khác 1 và các số thực α , β . Đẳng thức nào sau đây là sai?
A. a α . a β = a α . β
B. a α . a β = a α + β
C. a α β = a α . β
D. a α a β = a α − β
Nếu a, b, c là các số thực bất kì và a < b thì bất đẳng thức nào sau đây luôn đúng?
A. 2 a + 5 c < 2 b + 5 c
B. a 2 < b 2
C. a c > b c
D. a c < b c
Do a< b mà 2 > 0 nên 2a < 2b (*)
Cộng cả 2 vế của (*) với 5c ta được: 2a + 5c < 2b + 5c
Sử dụng bất đẳng thức để viết các mệnh đề sau
a) x là số dương.
b) y là số không âm.
c) Với mọi số thực α, |α| là số không âm.
d) Trung bình cộng của hai số dương a và b không nhỏ hơn trung bình nhân của chúng.
a) x > 0
b) y ≥ 0
c) ∀α ∈ R, |α| ≥ 0
d) ∀a, b > 0, 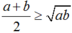
Với a,b,c là các số dương, a ≠ 1 đẳng thức nào sau đây sai?
![]()
![]()
![]()
![]()
Nếu a, b và c là các số bất kì và a > b thì bất đẳng thức nào sau đây luôn đúng?
A. a c > b c
B. a 2 > b 2
C. a + c > b + c
D. c - a > c - b
Áp dụng tính chất: Nếu a > b và c là số bất kì thì a + c > b + c.
Có thể lấy ví dụ để thấy các bất đẳng thức còn lại không đúng. ( bỏ đi)
Đáp án là C.
CMR với bất kì các số thực dương a,b,c sao cho a+b+c=ab+bc+ac , bất đẳng thức sau đây xảy ra :
\(3+\sqrt[3]{\dfrac{a^3+1}{2}}+\sqrt[3]{\dfrac{b^3+1}{2}}+\sqrt[3]{\dfrac{c^3+1}{2}}\le2\left(a+b+c\right)\)
Với a, b, c là các số thực dương, a và c khác 1 và α ≠ 0. Mệnh đề nào dưới đây sai?
A. log a b . log c a = log c b
B. log a α b = α log a b
C. log a b c = log a b - log a c
D. log a b c = log a b + log a c
Đáp án B
Phương pháp:
Sử dụng các công thức liên quan đến logarit.
Cách giải:
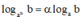 : là mệnh đề sai.
: là mệnh đề sai.
![]()
Biết rằng a là số thực dương sao cho bất đẳng thức 3 x + a x ⩾ 6 x + 9 x đúng với mọi số thực x. Mệnh đề nào sau đây đúng?
![]()
![]()
![]()
![]()