Cho ∆ A B C và điểm M thỏa mãn B M → = 2 C M → . F là một phép dời hình. Gọi A 1 = F ( A ) , B 1 = F ( B ) , C 1 = F ( C ) , M 1 = F ( M ) . Biết A B = 4 , B C = 5 , A C = 6 . Khi đó độ dài đoạn A 1 M 1 bằng:
A. 106
B. 138
C. 122
D. 38
Những câu hỏi liên quan
a) CHO 3 SỐ DƯƠNG a , b , c THỎA MÃN abc=1 . CMR: (a+b)(b+c)(c+a)>= 2(1+a+b+c)
b) CHO m,n LÀ 2 SỐ NGUYÊN DƯƠNG THỎA MÃN: m^2+n^2+2018 CHIA HẾT CHO mn. CMR m,n LÀ 2 SỐ LẺ VÀ NGUYÊN TỐ CÙNG NHAU
m.n/(m^2+n^2 ) và m.n/2018
- Đặt (m,n)=d => m= da;n=db ; (a,b)=1
=> d^2(a^2+b^2)/(d^2(ab)) = (a^2+b^2)/(ab) => b/a ; a/b => a=b=> m=n=> ( 2n^2+2018)/n^2 =2 + 2018/n^2 => n^2/2018
=> m=n=1 ; lẻ và nguyên tố cùng nhau. vì d=1
Đúng 0
Bình luận (0)
Vẽ SH _I_ (ABCD) => H là trung điểm AD => CD _I_ (SAD)
Vẽ HK _I_ SD ( K thuộc SD) => CD _I_ HK => HK _I_ (SCD)
Vẽ AE _I_ SD ( E thuộc SD).
Ta có S(ABCD) = 2a² => SH = 3V(S.ABCD)/S(ABCD) = 3(4a³/3)/(2a²) = 2a
1/HK² = 1/SH² + 1/DH² = 1/4a² + 1/(a²/2) = 9/4a² => HK = 2a/3
Do AB//CD => AB//(SCD) => khoảng cách từ B đến (SCD) = khoảng cách từ A đến (SCD) = AE = 2HK = 4a/3
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho ba điểm A (-1; 0; 1), B (3; 2; 1), C (5; 3; 7). Gọi M (a; b; c) là điểm thỏa mãn MA MB và MB + MC đạt giá trị nhỏ nhất. Tính P a + b + c A. P 4 B. P 0 C. P 2 D. P 5
Đọc tiếp
Trong không gian Oxyz, cho ba điểm A (-1; 0; 1), B (3; 2; 1), C (5; 3; 7). Gọi M (a; b; c) là điểm thỏa mãn MA = MB và MB + MC đạt giá trị nhỏ nhất. Tính P = a + b + c
A. P = 4
B. P = 0
C. P = 2
D. P = 5
Chọn D
Gọi I là trung điểm của AB, suy ra I (1;1;1); 
Phương trình mặt phẳng trung trực của AB: (α): 2x + y -3 = 0.
Vì (2.3 + 1.2 - 3). (2.5 + 1.3 - 3) = 50 > 0 nên B, C nằm về một phía so với (α), suy ra A, C nằm về hai phía so với (α).
Điểm M thỏa mãn MA = MB khi M ∈ (α).
Khi đó MB + MC = MA + MC ≥ AC.
MB + MC nhỏ nhất bằng AC khi M = AC ∩ (α)
Phương trình đường thẳng AC: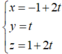 
do đó tọa độ điểm M là nghiệm của hệ phương trình
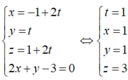
Do đó M (1; 1; 3), a + b + c = 5
Đúng 0
Bình luận (0)
Cho hàm số
y
2
x
-
2
x
-
2
có đồ thị là (C).M là điểm thuộc (C) sao cho tiếp tuyến của (C) tại M cắt hai đường tiệm cận của (C) tại hai điểm A, B thỏa mãn
AB...
Đọc tiếp
Cho hàm số y = 2 x - 2 x - 2 có đồ thị là (C).M là điểm thuộc (C) sao cho tiếp tuyến của (C) tại M cắt hai đường tiệm cận của (C) tại hai điểm A, B thỏa mãn AB = 2 5 . Gọi S là tổng các hoành độ của tất cả các điểm M thỏa mãn bài toán. Giá trị của S bằng:
A. 8
B. 5
C. 7
D. 6
Cho hàm số
y
2
x
−
2
x
−
2
có đồ thị là (C). M là điểm thuộc (C) sao cho tiếp tuyến của (C) tại M cắt hai đường tiệm cận của (C) tại hai điểm A, B thỏa mãn
A
B
2
5
. Gọi S là tổng các hoành độ của tất cả các điểm M thỏa mãn bài toán. Giá trị của S bằng: A. 8...
Đọc tiếp
Cho hàm số y = 2 x − 2 x − 2 có đồ thị là (C). M là điểm thuộc (C) sao cho tiếp tuyến của (C) tại M cắt hai đường tiệm cận của (C) tại hai điểm A, B thỏa mãn A B = 2 5 . Gọi S là tổng các hoành độ của tất cả các điểm M thỏa mãn bài toán. Giá trị của S bằng:
A. 8
B. 5
C. 7
D. 6
Cho 5 điểm A,B,C,D,M và N thỏa mãn: 3 điểm A,B,C thẳng hàng; 3 điểm A,B,M không thẳng hàng và 3 điểm A,B,N thẳng hàng.
a, Vẽ hình minh họa
b,Chứng tỏ 4 điểm A,B,C và N cùng thuộc 1 đường thẳng
c, Có bao nhiêu đg thẳn phân biệt đi qua 2 điểm trong 5 điểm đã cho? Kể tên
Trong không gian tọa độ Oxyz, cho A(2;0;0),B(0;2;0),C(0;0;2). Có tất cả bao nhiêu điểm M trong không gian thỏa mãn M không trùng với các điểm A, B, C và
A
M
B
^
B
M
C
^
C
M
A
^
90
o...
Đọc tiếp
Trong không gian tọa độ Oxyz, cho A(2;0;0),B(0;2;0),C(0;0;2). Có tất cả bao nhiêu điểm M trong không gian thỏa mãn M không trùng với các điểm A, B, C và A M B ^ = B M C ^ = C M A ^ = 90 o
A. 0
B. 1
C. 2
D. 3
Cho a,b,c>0 thỏa mãn \(a^2=b^2+c^2\). CMR
a) \(a^m>b^m+c^m\) nếu m>2
b) \(a^m< b^m+c^m\) nếu m<2
Sử dụng tính đơn điệu của hàm mũ: hàm \(y=a^x\) nghịch biến khi \(0< a< 1\) và đồng biến khi \(a>1\)
\(a^2=b^2+c^2\Rightarrow\left(\dfrac{b}{a}\right)^2+\left(\dfrac{c}{a}\right)^2=1\)
\(\Rightarrow\left\{{}\begin{matrix}0< \dfrac{b}{a}< 1\\0< \dfrac{c}{a}< 1\end{matrix}\right.\) nên các hàm \(\left(\dfrac{b}{a}\right)^x\) và \(\left(\dfrac{c}{a}\right)^x\) đều nghịch biến
Xét: \(\dfrac{b^m+c^m}{a^m}=\left(\dfrac{b}{a}\right)^m+\left(\dfrac{c}{a}\right)^m\) \(\)
- Khi \(m>2\Rightarrow\left(\dfrac{b}{a}\right)^m< \left(\dfrac{b}{a}\right)^2\) và \(\left(\dfrac{c}{a}\right)^m< \left(\dfrac{c}{a}\right)^2\)
\(\Rightarrow\left(\dfrac{b}{a}\right)^m+\left(\dfrac{c}{a}\right)^m< \left(\dfrac{b}{a}\right)^2+\left(\dfrac{c}{a}\right)^2=1\)
Hay \(\dfrac{b^m+c^m}{a^m}< 1\) \(\Rightarrow a^m>b^m+c^m\)
Câu b c/m tương tự, \(m< 2\) thì \(\left(\dfrac{b}{a}\right)^m>\left(\dfrac{b}{a}\right)^2...\)
Đúng 2
Bình luận (4)
a) Cho A(1;-2), B(-3;4) và điểm M thỏa mãn \(\overrightarrow{AM}=\overrightarrow{OA}-2\overrightarrow{MB}\). Tìm tọa độ điểm M?
b) Cho A(1;-2), B(-5;0) và điểm M thỏa mãn \(\overrightarrow{MA}=3\overrightarrow{OA}-2\overrightarrow{MB}\). Tìm tọa độ điểm M?
Cho 5 điểm A,B,C,D,M và N thỏa mãn: 3 điểm A,B,C thẳng hàng; 3 điểm A,B,M không thẳng hàng và 3 điểm A,B,N thẳng hàng.
a, Vẽ hình minh họa
b,Chứng tỏ 4 điểm A,B,C và N cùng thuộc 1 đường thẳng
c, Có bao nhiêu đg thẳng phân biệt đi qua 2 điểm trong 5 điểm đã cho? Kể tên
CẦN GẤP
a) Cho hai điểm B,C phân biệt. Tập hợp những điểm M thỏa mãn overrightarrow{CM}.overrightarrow{CB}overrightarrow{CM}^2 làb) Cho 3 điểm A,B,C phân biệt . Tập hợp những điểm M mà overrightarrow{CM}.overrightarrow{CB}overrightarrow{CA}.overrightarrow{CB} LÀc) Cho tam giác ABC, điểm J thỏa mãn overrightarrow{AK}3overrightarrow{AJ}, I là trung điểm của cạnh AB, điểm K thỏa mãn overrightarrow{KA}+overrightarrow{KB}+2overrightarrow{KC}overrightarrow{0}. Một điểm M thay đỏi nhưng luôn thỏa mãn left(3ove...
Đọc tiếp
a) Cho hai điểm B,C phân biệt. Tập hợp những điểm M thỏa mãn \(\overrightarrow{CM}.\overrightarrow{CB}=\overrightarrow{CM}^2\) là
b) Cho 3 điểm A,B,C phân biệt . Tập hợp những điểm M mà \(\overrightarrow{CM}.\overrightarrow{CB}=\overrightarrow{CA}.\overrightarrow{CB}\) LÀ
c) Cho tam giác ABC, điểm J thỏa mãn \(\overrightarrow{AK}=3\overrightarrow{AJ}\), I là trung điểm của cạnh AB, điểm K thỏa mãn \(\overrightarrow{KA}+\overrightarrow{KB}+2\overrightarrow{KC}=\overrightarrow{0}\). Một điểm M thay đỏi nhưng luôn thỏa mãn \(\left(3\overrightarrow{MK}+\overrightarrow{AK}\right).\left(\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}\right)=0\). Tập hợp điểm M là đường nào