Hàm số nào trong các hàm số sau đồng biến trên R. A.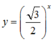 B. 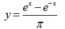C. . D.
Đọc tiếp
Hàm số nào trong các hàm số sau đồng biến trên R.
A.
B. 
C. 
.
D. 
Những câu hỏi liên quan
16 tháng 12 2021 lúc 19:51
cho hàm số y= x3. Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên \(R\)
B. Hàm số đồng biến trên \(R\)
C. Hàm số đồng biến trên (-∞;0)
D. Hàm số nghịch biến trên (0;+∞)
Cho hàm số y = x3 + 3x2 – 9x – 7 . Khẳng định nào sau đây là khẳng định sai?
A. Hàm số nghịch biến trên khoảng (-3;1) .
B. Hàm số đồng biến trên (-9;-5).
C. Hàm số đồng biến trên R.
D. Hàm số đồng biến trên (5;+∞).
Tập xác định: D = R.
Ta có: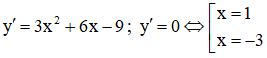 
Bảng biến thiên:
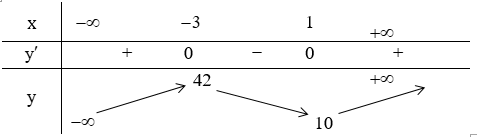
Kết luận: Hàm số đồng biến trên các khoảng: (-∞;-3),(1;+∞) . Hàm số nghịch biến trên khoảng (-3;1)
Chọn C.
Đúng 1
Bình luận (0)
Khẳng định nào sau đây đúng?
A. y = sin3x là hàm số chẵn
B. Hàm số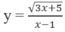 
xác định trên R
C. Hàm số y = x 3 + 4x - 5 đồng biến trên R
D. Hàm số y = sinx + 3x - 1 nghịch biến trên R
Khẳng định nào sau đây đúng?A. y sin3x là hàm số chẵnB. Hàm số
y
3
x
+
5
x
-
1
xác định trên RC. Hàm số y
x
3
+ 4x - 5 đồng biến trên RD. Hàm số y sinx + 3x - 1 nghịc...
Đọc tiếp
Khẳng định nào sau đây đúng?
A. y = sin3x là hàm số chẵn
B. Hàm số y = 3 x + 5 x - 1 xác định trên R
C. Hàm số y = x 3 + 4x - 5 đồng biến trên R
D. Hàm số y = sinx + 3x - 1 nghịch biến trên R
Đáp án: C.
Vì y' = 3 x 2 + 4 > 0, ∀ x ∈ R.
Đúng 0
Bình luận (0)
Trong các hàm số sau, hàm số nào đồng biến trên R? A.
y
2
3
x
B.
y
2
3
x
C.
y
0
,
99
x
D.
y...
Đọc tiếp
Trong các hàm số sau, hàm số nào đồng biến trên R?
A. y = 2 3 x
B. y = 2 3 x
C. y = 0 , 99 x
D. y = 2 - 3 x
Đáp án B
Phương pháp:
Xét hàm số y = ax, 0 < a ≠ 1
+) a > 1: Hàm số đồng biến trên R.
+) 0 < a < 1: Hàm số nghịch biến trên R.
Cách giải:
Hàm số nào đồng biến trên R là: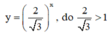 
Đúng 0
Bình luận (0)
Trong các hàm số sau, hàm số nào đồng biến trên R? A.
y
x
2
+
x
B.
y
x
4
+
x
2
C.
y
x
3
+
x
D.
y
x
+
1
x
+...
Đọc tiếp
Trong các hàm số sau, hàm số nào đồng biến trên R?
A. y = x 2 + x
B. y = x 4 + x 2
C. y = x 3 + x
D. y = x + 1 x + 3
Hàm số nào trong các hàm số sau đồng biến trên R? A.
y
7
x
-
2
sin
3
x
B.
y
x
3
+
2
x
2
+
1
C.
y
tan
x
D.
y
4
x
+...
Đọc tiếp
Hàm số nào trong các hàm số sau đồng biến trên R?
A. y = 7 x - 2 sin 3 x
B. y = x 3 + 2 x 2 + 1
C. y = tan x
D. y = 4 x + 1 x + 2
Trong các hàm số sau, hàm số nào đồng biến trên R: A.
y
x
3
+
3
x
2
+
3
x
+
2008
B.
y
x
4
+
x
2
+
2008
C.
y
c
o
t
x
D.
y...
Đọc tiếp
Trong các hàm số sau, hàm số nào đồng biến trên R:
A. y = x 3 + 3 x 2 + 3 x + 2008
B. y = x 4 + x 2 + 2008
C. y = c o t x
D. y = x + 1 x - 2
Trong các hàm số sau, hàm số nào đồng biến trên R?
Đọc tiếp
Trong các hàm số sau, hàm số nào đồng biến trên R?
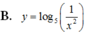
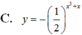
