Ai giúp mình cách tìm GTLN, GTNN với.
HELP ME!
Giup mình
Ai chỉ giúp mình cách tìm GTNN,GTLN của biểu thức mình cho 3 tick mỗi ngày, hứa danh dự!
Ai chỉ giúp mình cách tìm GTNN và GTLN của 1 biểu thức với?
cảm ơn!!!
Bạn làm nhiều bài tập rồi quen dần với mấy dạng này ,chứ chỉ ra cách nào thì khó lắm
Thường thì biến đổi về. Dạng bình phương (cũng có những cách khác nhé)
Ví du:tim giá trị nhỏ nhất của:x^2+2x+2=(x+1)^2+1 lớn hơn hoặc bằng 1 với mọi x thuộc R
Tìm giá GTLN hoặc GTNN của phép tính;
B=(3+4.x)^2+(y+2)^6+4
Ai làm đc thì giúp mình nha.
Ai nhanh mình sẽ tick cho.
Tìm gtln và gtnn ạ. Mình cần xem cách giải ạ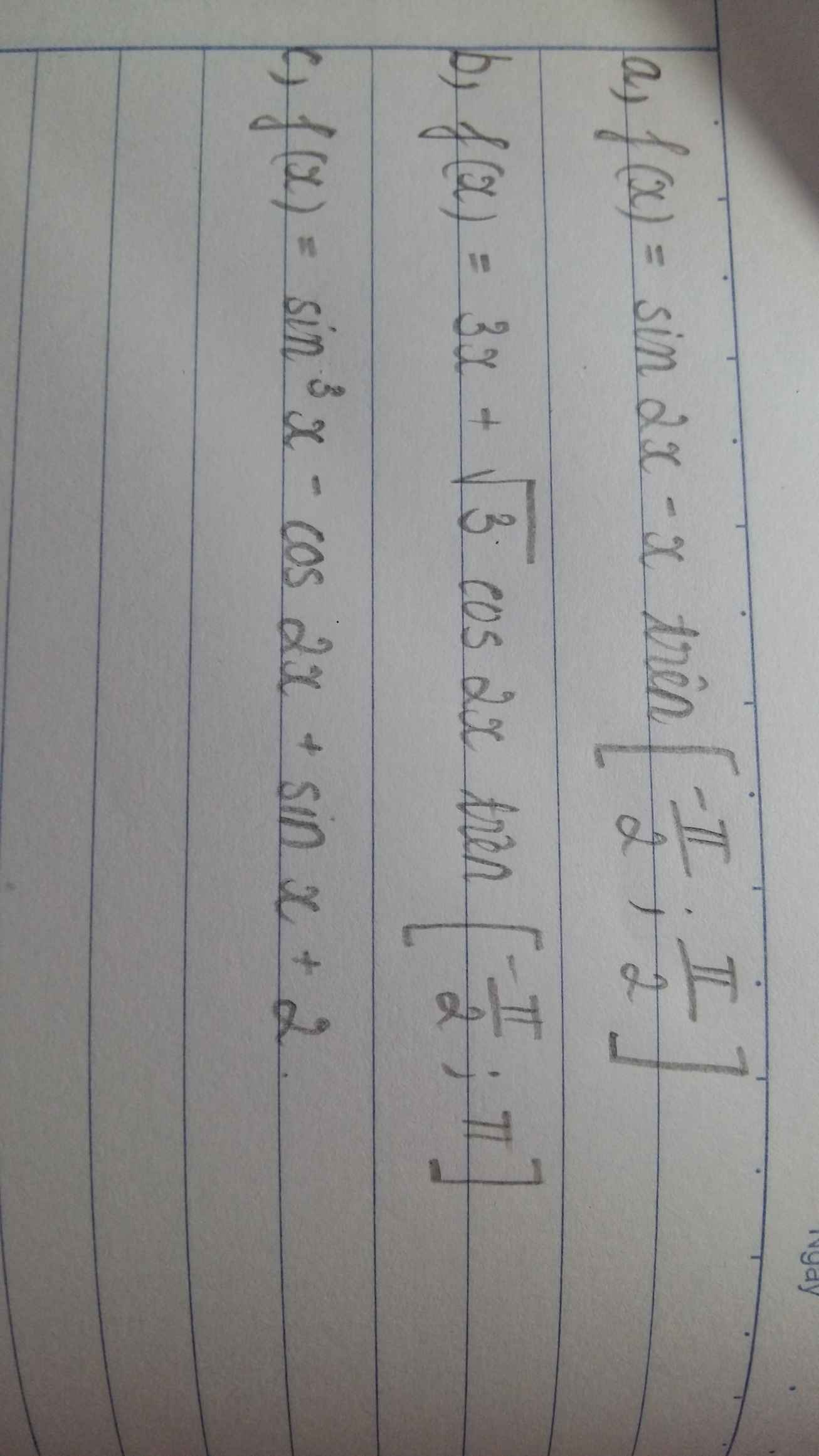
a.
\(f'\left(x\right)=2cos2x-1=0\Rightarrow cos2x=\dfrac{1}{2}\)
\(\Rightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{3}+k2\pi\\2x=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=-\dfrac{\pi}{6}+k\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}\\x=-\dfrac{\pi}{6}\end{matrix}\right.\)
Ta có:
\(f\left(-\dfrac{\pi}{2}\right)=0+\dfrac{\pi}{2}=\dfrac{\pi}{2}\)
\(f\left(\dfrac{\pi}{2}\right)=0-\dfrac{\pi}{2}=-\dfrac{\pi}{2}\)
\(f\left(\dfrac{\pi}{6}\right)=\dfrac{\sqrt{3}}{2}-\dfrac{\pi}{6}\)
\(f\left(-\dfrac{\pi}{6}\right)=-\dfrac{\sqrt{3}}{2}+\dfrac{\pi}{6}\)
So sánh các giá trị trên ta được:
\(f\left(x\right)_{max}=f\left(-\dfrac{\pi}{2}\right)=\dfrac{\pi}{2}\)
\(f\left(x\right)_{min}=f\left(\dfrac{\pi}{2}\right)=-\dfrac{\pi}{2}\)
b.
\(f'\left(x\right)=3-2\sqrt{3}sin2x=0\Rightarrow sin2x=\dfrac{\sqrt{3}}{2}\)
\(\Rightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{3}+k2\pi\\2x=\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=\dfrac{\pi}{3}+k\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}\\x=\dfrac{\pi}{3}\end{matrix}\right.\)
Ta có: \(f\left(-\dfrac{\pi}{2}\right)=-\dfrac{3\pi}{2}-\sqrt{3}\)
\(f\left(\dfrac{\pi}{6}\right)=\dfrac{\pi}{2}+\dfrac{\sqrt{3}}{2}\)
\(f\left(\dfrac{\pi}{3}\right)=\pi-\dfrac{\sqrt{3}}{2}\)
\(f\left(\pi\right)=3\pi+\sqrt{3}\)
Từ đó: \(f_{min}=f\left(-\dfrac{\pi}{2}\right)=-\dfrac{3\pi}{2}-\sqrt{3}\)
\(f_{max}=f\left(\pi\right)=3\pi+\sqrt{3}\)
c.
\(f\left(x\right)=sin^3x-\left(1-2sin^2x\right)+sinx+2=sin^3x+2sin^2x+sinx+1\)
Đặt \(sinx=t\Rightarrow t\in\left[-1;1\right]\)
Xét hàm \(f\left(t\right)=t^3+2t^2+t+1\) trên \(\left[-1;1\right]\)
\(f'\left(t\right)=3t^2+4t+1=0\Rightarrow\left[{}\begin{matrix}t=-1\\t=-\dfrac{1}{3}\end{matrix}\right.\)
\(f\left(-1\right)=1\) ; \(f\left(-\dfrac{1}{3}\right)=\dfrac{23}{27}\) ; \(f\left(1\right)=5\)
\(\Rightarrow f_{max}=5\) ; \(f_{min}=\dfrac{23}{27}\)
các bạn cho mình hỏi cách tìm GTNN và GTLN
Để tìm GTNN và GTLN thì :
VD : \(\left(x+8\right)^2+2\) tìm gtnn
Ta có : \(\left(x+8\right)^2\ge0\) ( vì 2 nên phải lớn hơn không )
\(\Rightarrow\left(x+8\right)^2+2\ge2\)( +2 thì bên kia cũng cộng 2 )
Lớn hơn 2 \(\Rightarrow GTNN\) là 2 khi \(x+8=0\)
\(x=-8\)
GTLN cũng z
chỉ giùm mình cách tìm GTNN và GTLN đi m bn
VD như: Tìm GTNN của /x-1/2/
Ta có :
|x - 1/2| > 0
Vậy GTNN của |x - 1/2| = 0 <=> x - 1/2 = 0 <=> x = 1/2
Ai chỉ mình cách tìm GTNN, GTLN của biểu thức hay phân số với
Mình tick cho 7 cái luôn, hứa danh dự
Mong ONLINEMATH đừng trừ điểm
Mình cảm ơn nhiều!
dễ làm mà cũng không biết tick mình 7 cái rồi mình chỉ cho
LƯU Ý
Các bạn học sinh KHÔNG ĐƯỢC đăng các câu hỏi không liên quan đến Toán, hoặc các bài toán linh tinh gây nhiễu diễn đàn (như 1+1 = ?). Online Math có thể áp dụng các biện pháp như trừ điểm, thậm chí khóa vĩnh viễn tài khoản của bạn nếu vi phạm nội quy nhiều lần.
Chuyên mục Giúp tôi giải toán dành cho những bạn gặp bài toán khó hoặc có bài toán hay muốn chia sẻ. Bởi vậy các bạn học sinh chú ý không nên gửi bài linh tinh, không được có các hành vi nhằm gian lận điểm hỏi đáp như tạo câu hỏi và tự trả lời rồi chọn đúng.
Mỗi thành viên được gửi tối đa 5 câu hỏi trong 1 ngày
mn cho mình hỏi cách tings GTLN, GTNN của 1 đa thức vs . nhìu bài khó wa' mình ko làm được . Giúp mình đi mình tick cho
các bạn giúp mình bài này theo cách làm lớp 11 với ạ. Tìm GTLN, GTNN của:

ta có \(x\in\left[-\frac{\pi}{4};0\right]\Rightarrow2x\in\left[-\frac{\pi}{2},0\right]\Rightarrow sin2x\in\left[-1,0\right]\)
Vậy \(\hept{\begin{cases}GTNN=-1\\GTLN=0\end{cases}}\)