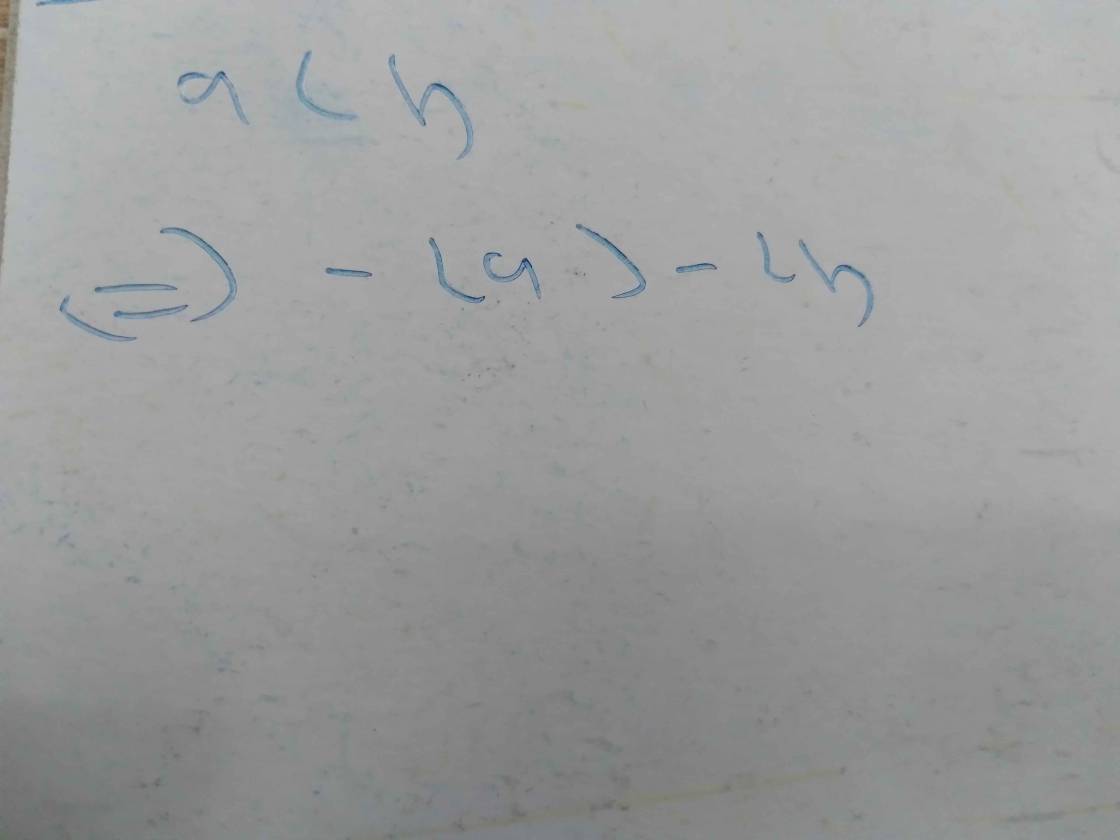a) Từ a < b => 2a < 2b (nhân hai vế với 2 > 0)

=> 2a + 1 < 2b + 1 (*) (cộng hai vế với 1)

b) Ta có 2b + 1 < 2b + 3 với mọi số thực b.

Kết hợp với (*) ta suy ra:

2a + 1 < 2b + 3 (tính chất bắc cầu)

a < b

⇒ 2a < 2b (nhân hai vế với 2 > 0, BĐT không đổi chiều)

⇒ 2a + 1 < 2b + 1 (cộng hai vế với 1).

Vậy 2a + 1 < 2b + 1.

Vì a > b

=> 2a > 2b

Mà 3 > 1

=> 2a + 3 > 2b + 1

Vậy 2a + 3 > 2b + 1

Vì a>b suy ra 2a>2b (1)

mà 3 >1  (2)

nên từ (1) và (2) suy ra 2a+3 > 2b +1.

a>b => 2a>2b

Mà : 3>1

Hay : 2a+3>2b+1  (BĐT)

=> đpcm 

a: a>b

=>3a>3b

=>3a+5>3b+5

b: a>b

=>2a>2b

=>2a-3>2b-3>2b-4

2a < 2b              2a < a+b                -a > -b

\(a< b\)

\(\Leftrightarrow2a< 2b\)

\(a< b\)

\(\Leftrightarrow a+a< b+a\)

\(\Leftrightarrow2a< a+b\)

\(a< b\)

\(\Leftrightarrow-1a>-1b\)

\(\Leftrightarrow-a>-b\)

Do \(a< b\) , nên :

Gọi \(a=2,b=3\)

+ \(2a\Leftrightarrow2.2=4\)

   \(2b=2.3=6\)

   Mà \(4< 6\) \(\Rightarrow2a< 2b\)

+ \(2a\Leftrightarrow2.2=4\)

   \(a+b\Leftrightarrow2+3=5\)

   Mà \(4< 5\) \(\Rightarrow2a< a+b\)

+ \(-a\Leftrightarrow-1.2=-2\)

   \(-b\Leftrightarrow-1.3=-3\)

   Mà \(-2>-3\) \(\Rightarrow-a>-b\)

a) 3a + 5 > 3b + 5;          b) 2a - 3 > 2b - 4

+ a < b ⇒ 2a < 2b (nhân cả hai vế với 2 > 0, BĐT không đổi chiều).

+ a < b ⇒ a + a < b + a (Cộng cả hai vế với a)

hay 2a < a + b.

+ a < b ⇒ (-1).a > (-1).b (Nhân cả hai vế với -1 < 0, BĐT đổi chiều).

hay –a > -b.

Vì a<b

nên -2a > -2b ( nhân cả 2 vế với  -2)

Có a<b nên -2a>-2b ( nhân cả 2 vế với -2 )

a/ ta có : a<b

=> 2a<2b

=>2a-1<2b-1