Cho hai mặt phẳng ( P ) : ( m - 1 ) x + 2 y – z + 10 = 0 v à ( Q ) : - x + ( 2 m + 1 ) y – m z + 2 = 0 . Tìm m để hai mặt phẳng trên vuông góc với nhau.
A. m = - 3 4
B. m = 3 4
C. m = 4 3
D. m = - 4 3
Những câu hỏi liên quan
Trong không gian Oxyz, cho hai mặt phẳng
(
P
)
:
2
x
-
m
y
-
4
z
-
6
+
m
0
v
à
(
Q
)
:
(
m
+
3
)...
Đọc tiếp
Trong không gian Oxyz, cho hai mặt phẳng ( P ) : 2 x - m y - 4 z - 6 + m = 0 v à ( Q ) : ( m + 3 ) x + y + ( 5 m + 1 ) z - 7 = 0 . Tìm m để hai mặt phẳng (P) và (Q) trùng nhau
A. m = - 6 5
B. m = 1
C. m = -1
D. m = 4
Chọn C.
Để hai mặt phẳng (P) và (Q) trùng nhau khi và chỉ khi:
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho hai mặt phẳng: (P): x - 2y - 2z + 1 0, (Q): 2x - 4y - 4z + m 0. Tìm các giá trị của m biết rằng khoảng cách giữa hai mặt phẳng (P) và (Q) bằng 1 A. m8 B. m38 C. m8 hoặc m-4 D. m38 hoặc m-34
Đọc tiếp
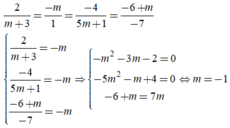
Trong không gian Oxyz, cho hai mặt phẳng: (P): x - 2y - 2z + 1 = 0, (Q): 2x - 4y - 4z + m = 0. Tìm các giá trị của m biết rằng khoảng cách giữa hai mặt phẳng (P) và (Q) bằng 1
A. m=8
B. m=38
C. m=8 hoặc m=-4
D. m=38 hoặc m=-34
Trong không gian với hệ tọa độ Oxyz cho hai mặt phẳng
(
P
)
:
x
+
2
y
-
2
z
+
1
0
,
Q
:
x
+
m
y
+
m
-
1
z
+
2019
0
. Khi hai mặt phẳng
P
,...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho hai mặt phẳng ( P ) : x + 2 y - 2 z + 1 = 0 , Q : x + m y + m - 1 z + 2019 = 0 . Khi hai mặt phẳng P , Q tạo với nhau một góc nhỏ nhất thì mặt phẳng (Q) đi qua điểm M nào sau đây?
A. M 2019 , - 1 , 1
B. M 0 . - 2019 , 0
C. M - 2019 , 1 , 1
D. M 0 , 0 - 2019
Gọi n p → ; n Q → lần lượt là các VTPT của (P) và (Q) ta có
Khi đó ta có
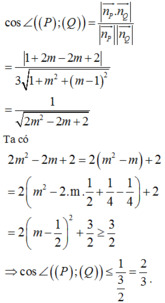
Dấu “=” xảy ra
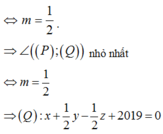
Khi đó (Q) đi qua điểm
Chọn C.
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P): x + 2 y - z - 1 0 , (Q): 3x-(m+2)y+(2m-1)z+30. Tìm m để hai mặt phẳng (P), (Q) vuông góc với nhau.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P): x + 2 y - z - 1 = 0 , (Q): 3x-(m+2)y+(2m-1)z+3=0. Tìm m để hai mặt phẳng (P), (Q) vuông góc với nhau.
Trong không gian Oxyz, cho hai mặt phẳng (P) và (Q) lần lượt có phương trình là x + my + (m + 3)z + 1 0; x - y + 2z 0, trong đó m là tham số. Với những giá trị nào của m thì mặt phẳng (P) vuông góc với mặt phẳng (Q)? A. m -1 B. m 0 C. m -7 D. Không tồn tại m
Đọc tiếp
Trong không gian Oxyz, cho hai mặt phẳng (P) và (Q) lần lượt có phương trình là x + my + (m + 3)z + 1 = 0; x - y + 2z = 0, trong đó m là tham số. Với những giá trị nào của m thì mặt phẳng (P) vuông góc với mặt phẳng (Q)?
A. m = -1
B. m = 0
C. m = -7
D. Không tồn tại m
Đáp án C
Ta có: n p → = (1; m; m + 3), n Q → = (1; -1; 2).
Hai mặt phẳng (P) và (Q) vuông góc khi và chỉ khi n p → . n Q → = 0
⇔ 1.1 + m.(-1) + (m + 3).2 = 0 ⇔ m + 7 = 0 ⇔ m = -7
Đúng 0
Bình luận (0)
Trong không gian với hệ toạ độ oxyz, cho hai mặt phẳng (P) : x+2y+z+1 0(Q): 2x-y+2z+4 0 Gọi M là điểm thuộc mặt phẳng (P) sao cho điểm đối xứng của M qua mặt phẳng (Q) nằm trên trục hoành. Tung độ của M bằng A. 4 B. 2 C. -3 D. -5
Đọc tiếp
Trong không gian với hệ toạ độ oxyz, cho hai mặt phẳng (P) : x+2y+z+1 = 0(Q): 2x-y+2z+4 = 0 Gọi M là điểm thuộc mặt phẳng (P) sao cho điểm đối xứng của M qua mặt phẳng (Q) nằm trên trục hoành. Tung độ của M bằng
A. 4
B. 2
C. -3
D. -5
Cho hai mặt phẳng
(
P
)
:
x
−
m
2
y
+
2
z
+
m
−
3
2
0
;
(
Q
)
:
2
x
−
8
y
+
4
z
+
1
0
,
với m là tham số thực. Tìm tất cả các giá trị của tham...
Đọc tiếp
Cho hai mặt phẳng ( P ) : x − m 2 y + 2 z + m − 3 2 = 0 ; ( Q ) : 2 x − 8 y + 4 z + 1 = 0 , với m là tham số thực. Tìm tất cả các giá trị của tham số m để hai mặt phẳng trên song song với nhau.
A. m = ± 2
B. Không tồn tại m
C. m = 2
D. m = − 2
Đáp án D.
Đề 2 mặt phẳng song song với nhau thì 1 2 = − m 2 − 8 = 2 4 ≠ m − 3 2 ⇒ m = − 2.
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (S): x + 2y – 2z + 2018 0 và (Q): x + my (m -1)z + 2017 0. Khi hai mặt phẳng (P) và (Q) tạo với nhau một góc nhỏ nhất thì điểm H nào dưới đây nằm trong mặt phẳng (Q)? A. H (-2017; 1; 1) B. H (2017; -1; 1) C. H (-2017; 0; 0) D. H (0; -2017; 0)
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (S): x + 2y – 2z + 2018 = 0 và (Q): x + my (m -1)z + 2017 = 0. Khi hai mặt phẳng (P) và (Q) tạo với nhau một góc nhỏ nhất thì điểm H nào dưới đây nằm trong mặt phẳng (Q)?
A. H (-2017; 1; 1)
B. H (2017; -1; 1)
C. H (-2017; 0; 0)
D. H (0; -2017; 0)
Chọn A
Vectơ pháp tuyến của (P) và (Q) lần lượt là
Gọi φ là góc tạo bởi hai mặt phẳng (P) và (Q) thì 00 ≤ φ ≤ 900
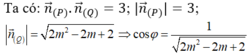
Để (P) và (Q) tạo với nhau một góc nhỏ nhất thì cosφ lớn nhất 
nhỏ nhất.
Mà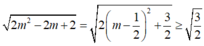 
nên giá trị lớn nhất của là 
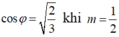khi m = 1/2
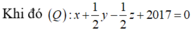
Vậy H (-2017; 1; 1) ∈ (Q)
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz cho hai mặt phẳng (P): x+2y+z+10 và (Q):2x-y+2z+40 . Gọi M là điểm thuộc mặt phẳng (P) sao cho điểm đối xứng của M qua mặt phẳng (Q) nằm trên trục hoành . Tung độ của điểm M bằng A. 4. B. 2. C. -5 D. 3
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho hai mặt phẳng (P): x+2y+z+1=0 và (Q):2x-y+2z+4=0 . Gọi M là điểm thuộc mặt phẳng (P) sao cho điểm đối xứng của M qua mặt phẳng (Q) nằm trên trục hoành . Tung độ của điểm M bằng
A. 4.
B. 2.
C. -5
D. 3
