Cho A O B ^ = 135 o . Vẽ B O C ^ và A O D ^ kề bù với A O B ^ . Chọn câu đúng nhất
A. B O C ^ và A O D ^ là hai góc đối đỉnh
B. B O C ^ = 45 °
C. Hai tia phân giác của hai góc B O C ^ và A O D ^ là hai tia đối nhau
D. Cả A,B,C đều đúng
Bài 1: cho hình vẽ biết AB// DE, \(\widehat{B}=115^o;\widehat{D}=135^o\) .Vẽ đường thẳng xy đi qua C và song song với AB.
a) chứng minh xy//DE
b) Tính số đo \(\widehat{BCD}\)
cho hình vẽ nào cơ
bạn phải đăng lên chứ
Tính:
\(A = \sin {150^o} + \tan {135^o} + \cot {45^o}\)
\(B = 2\cos {30^o} - 3\tan 150 + \cot {135^o}\)
\(A = \sin {150^o} + \tan {135^o} + \cot {45^o}\)
Sử dụng bảng giá trị lượng giác của một số góc đặc biệt, ta có:
\(\sin {150^o} = \frac{1}{2};\tan {135^o} = - 1;\cot {45^o} = 1.\)
\( \Rightarrow A = \frac{1}{2} - 1 + 1 = \frac{1}{2}.\)
\(B = 2\cos {30^o} - 3\tan 150 + \cot {135^o}\)
Sử dụng bảng giá trị lượng giác của một số góc đặc biệt, ta có:
\(\cos {30^o} = \frac{{\sqrt 3 }}{2};\tan {150^o} = - \frac{{\sqrt 3 }}{3};\cot {135^o} = - 1.\)
\( \Rightarrow B = 2.\frac{{\sqrt 3 }}{2} - 3.\left( { - \frac{{\sqrt 3 }}{3}} \right) + 1 = 2\sqrt 3 + 1.\)
Cho tam giác ABC có \(\widehat B = {135^o}\). Khẳng định nào sau đây là đúng?
c.
A. \({a^2} = {b^2} + {c^2} + \sqrt 2 ab.\)
B. \(\frac{b}{{\sin A}} = \frac{a}{{\sin B}}\)
C. \(\sin B = \frac{{ - \sqrt 2 }}{2}\)
D. \({b^2} = {c^2} + {a^2} - 2ca\cos {135^o}.\)
A. \({a^2} = {b^2} + {c^2} + \sqrt 2 ab.\) (Loại)
Vì: Theo định lí cos ta có: \({a^2} = {b^2} + {c^2} - 2bc.\cos A\)
Không đủ dữ kiện để suy ra \({a^2} = {b^2} + {c^2} + \sqrt 2 ab.\)
B. \(\frac{b}{{\sin A}} = \frac{a}{{\sin B}}\) (Loại)
Theo định lí sin, ta có: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} \nRightarrow \frac{b}{{\sin A}} = \frac{a}{{\sin B}}\)
C. \(\sin B = \frac{{ - \sqrt 2 }}{2}\)(sai vì theo câu a, \(\sin B = \frac{{\sqrt 2 }}{2}\))
D. \({b^2} = {c^2} + {a^2} - 2ca\cos {135^o}.\)
Theo định lý cos ta có:
\({b^2} = {c^2} + {a^2} - 2ca.\cos B\) (*)
Mà \(\widehat B = {135^o} \Rightarrow \cos B = \cos {135^o}\).
Thay vào (*) ta được: \({b^2} = {c^2} + {a^2} - 2ca\;\cos {135^o}\)
=> D đúng.
Chọn D
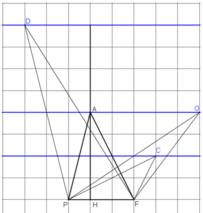
Tam giác PAF được vẽ trên giấy kẻ ô vuông (h.135). Hãy chỉ ra:
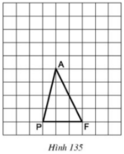
a) Một điểm I sao cho SPIF = SPAF
b) Một điểm O sao cho SPOF = 2.SPAF
c) Một điểm N sao cho 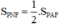
Gọi AH là chiều cao của tam giác APF.
Ta có: SAPF = AH.PF/2.
a) SPIF = SPAF
⇔ chiều cao IK = AH (Chung cạnh đáy PF).
⇔ I nằm trên đường thẳng song song với PF và cách PF 1 khoảng bằng AH.
b) SPOF = 2.SPAF
⇔ chiều cao OM = 2.AH
⇔ O nằm trên đường thẳng song song với PF và cách PF một khoảng bằng 2.AH
c) 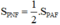
⇔ chiều cao NQ = AH/2
⇔ N nằm trên đường thẳng song song với PF và cách PF một khoảng bằng AH/2.
Trên đường thẳng AC lấy điểm B . Trên một nửa mặt phẳng bờ là đường thẳng AC , vẽ tia BD . Cho biết góc CBD = 3 lần góc ABD . Khi đó số đo góc CBD là ?
A.130 \(^o\)
B. 135\(^o\)
C. 140\(^o\)
D. 145\(^o\)
Vd5: Cho hai đường thẳng xx' và yy' cắt nhau tại O sao cho góc xOy = 135⁰, số đo của góc xOy' = ? A. 55⁰ B. 65⁰ C. 60⁰ D. 45⁰ Vd6: Cho góc xBy = 75⁰, vẽ góc x'By' đối đỉnh với góc xBy. Số đo góc x'By' bằng: A. 30⁰ B. 120⁰ C. 90⁰ D. 75⁰
Cho (O) ,đường kính BC , A là điểm di động đường tròn (O) . Gọi I là tâm đường tròn nội tiếp tam giác ABC .Khi A di chuyển trên (O) thì :
A, I thuộc cung chứa góc 135 độ dừng trên đoạn AB .
B, I thuộc cung chứa góc 135 độ dừng trên đoạn AC .
C, I thuộc cung chứa góc 135 độ dừng trên đoạn BC .
D, I thuộc cung chứa góc 45 độ dừng trên đoạn BC .
Cho (O) ,đường kính BC , A là điểm di động đường tròn (O) . Gọi I là tâm đường tròn nội tiếp tam giác ABC .Khi A di chuyển trên (O) thì :
A, I thuộc cung chứa góc 135 độ dừng trên đoạn AB .
B, I thuộc cung chứa góc 135 độ dừng trên đoạn AC .
C, I thuộc cung chứa góc 135 độ dừng trên đoạn BC .
D, I thuộc cung chứa góc 45 độ dừng trên đoạn BC .
Anh em giúp tôi mai mình kiểm tra rồi nhé
C nhé bạn
Công thức của nó có tính góc BIC = 90 + BAC/2=135
Cho góc AOB=120\(^o\) .Qua A vẽ tia Ax sao cho góc xAO =135\(^0\) ,qua B vẽ tia BY sao cho góc OBy=105\(^0\) (Ax và By cũng nằm trên 1 nửa mặt phẳng bờ AO)Chứng, minh:Ax//By
Help me!!!

Kẻ thêm tia Oz trong \(\widehat{AOB}\) sao cho Oz // By(1)
Ta có: Oz // By (cách dựng) \(\Rightarrow\widehat{B}+\widehat{O_1}=180^0\)( tổng 2 góc trong cùng phía)
\(\Leftrightarrow\widehat{O_1}=180^0-105^0=75^0\)
Ta có: \(\widehat{O_1}+\widehat{O_2}=120^0\)
\(\Leftrightarrow75^0+\widehat{O_2}=120^0\)
\(\Leftrightarrow\widehat{O_2}=120^0-75^0=45^0\)
Ta có: \(\widehat{O_2}+\widehat{A}=45^0+135^0=180^0\)
mà 2 góc ở vị trí trong cùng phía
=> Oz//Ax(2)
Từ (1), (2) => Ax//By
Cho đường thẳng xy đi qua điểm O. Vẽ tia Oz sao cho 0 xOz 135 . Trên nửa mặt phẳng bờ không chứa tia Oz, vẽ tia Ot sao cho 0 yOt 90 . Gọi Om là tia phân giác của góc xOt . a) Chứng minh rằng Om và Oz là hai tia đối nhau. b) 𝑚𝑂𝑡 ̂ và yOz có phải là hai góc đối đỉnh không? Vì sao?
Hình bn tự vẽ nha
Vì Ox, Oy là 2 tia đối nhau
Nên xOy=180*( góc bẹt)
Ta có: xOt+tOy=xOy=180*
=> xOt=180*-90*
=> xOt= 90*
Vì Ov là tia phân giác của góc xOt
=> tOv=vOx=xOt2=90độ2=45độxOt2=90độ2=45độ
=> Tia Ox nằm giữa 2 tia Ov và Oz
nên vOx +xOz=vOz
45*+135*=vOz
=> vOz=180*
b/ Vì Ox và Oy là 2 tia đối nhau nên
Ov và Oz là 2 tia đối nhau
Vậy xOv và zOy là 2 góc đối đỉnh
Vì Om là phân giác của \(\widehat{xOt}\) nên \(\widehat{xOm}=\widehat{mOt}=\dfrac{\widehat{xOt}}{2}=\dfrac{90^o}{2}=45^o\)(1)
Ta có: \(\widehat{xOz}+\widehat{zOy}=180^o\) (kề bù)
\(135^o+\widehat{zOy}=180^o\)
\(\widehat{zOy}=45^o\)(2)
Từ (1),(2)=> \(\widehat{zOy}=\widehat{xOm}\)
=> \(\widehat{zOy}\) và \(\widehat{xOm}\) là 2 góc đối đỉnh
=>Om và Oz đối nhau
b)\(\widehat{xOt}+\widehat{tOy}=180^o\)
\(90^o+\widehat{tOy}=180^o\)
\(\widehat{tOy}=90^o\)
=>\(Oy\perp Ot\)
Vậy Oy không đối Ot mà 2 góc đối đỉnh tạo nên từ cặp tia đối nên
\(\widehat{mOt}\) và \(\widehat{yOz}\) không đối đỉnh