Giá trị của m để bất phương trình 3x - 2m + 5 ≥ 0 có tập nghiệm là tập con của [2;+ ∞ ) là:
A. m ≥ 5 2
B. m ≤ 11 2
C. m ≤ 5 2
D. m ≥ 11 2
Những câu hỏi liên quan
Có bao nhiêu giá trị nguyên dương của tham số m để tập nghiệm của bất phương trình
(
3
x
+
2
-
3
)
(
3
x
-
2
m
)
0
chứa không quá 9 số nguyên? A. 3281. B. 3283. C. 3280. D. 3279.
Đọc tiếp
Có bao nhiêu giá trị nguyên dương của tham số m để tập nghiệm của bất phương trình ( 3 x + 2 - 3 ) ( 3 x - 2 m ) < 0 chứa không quá 9 số nguyên?
A. 3281.
B. 3283.
C. 3280.
D. 3279.
Cho phương trình
(
m
-
5
)
.
3
x
+
(
2
m
-
2
)
.
2
x
.
3
x
+
(
1
-
m
)
.
4
x
0
, tập hợp tất cả các giá trị của tham số m để phương trì...
Đọc tiếp
Cho phương trình ( m - 5 ) . 3 x + ( 2 m - 2 ) . 2 x . 3 x + ( 1 - m ) . 4 x = 0 , tập hợp tất cả các giá trị của tham số m để phương trình có hai nghiệm phân biệt là khoảng (a;b). Tính S=a+b
A.4
B.5
C.6
D.8
Tìm giá trị của m để bất phương trình x2 + 2mx - 2m +3 ≥ 0 có tập nghiệm R
\(x^2+2mx-2m+3>=0\)(1)
\(\text{Δ}=\left(2m\right)^2-4\cdot1\cdot\left(-2m+3\right)\)
\(=4m^2+8m-12\)
\(=4\left(m^2+2m-3\right)=4\left(m+3\right)\left(m-1\right)\)
Để bất phương trình (1) đúng với mọi x thuộc R thì \(\left\{{}\begin{matrix}\text{Δ}< =0\\a>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4\left(m+3\right)\left(m-1\right)< =0\\1>0\end{matrix}\right.\)
=>\(\left(m+3\right)\left(m-1\right)< =0\)
TH1: \(\left\{{}\begin{matrix}m+3>0\\m-1< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>-3\\m< 1\end{matrix}\right.\)
=>-3<m<1
TH2: \(\left\{{}\begin{matrix}m+3< 0\\m-1>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m< -3\\m>1\end{matrix}\right.\)
=>\(m\in\varnothing\)
Đúng 1
Bình luận (0)
Xét bất phương trình
3
3
x
-
4
.
3
x
+
1
+
3
m
-
5
0
. Tập hợp tất cả các giá trị thực của tham số m để bất phương trình đã cho có nghiệm thực là A.
(
-
∞
;
7
]
B.
-...
Đọc tiếp
Xét bất phương trình 3 3 x - 4 . 3 x + 1 + 3 m - 5 < 0 . Tập hợp tất cả các giá trị thực của tham số m để bất phương trình đã cho có nghiệm thực là
A. ( - ∞ ; 7 ]
B. - ∞ ; 5 3
C. - ∞ ; 3
D. - ∞ ; 7
Chọn đáp án D.
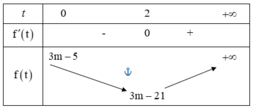
Từ bảng biến thiên trên, ta có bất phương trình đã cho có nghiệm khi và chỉ khi bất phương trình f(t) < 0
Đúng 0
Bình luận (0)
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m thuộc đoạn [-10;10] để bất phương trình
log
3
2
x
2
+
x
+
m
+
1
x
2
+
x
+
1...
Đọc tiếp
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m thuộc đoạn [-10;10] để bất phương trình log 3 2 x 2 + x + m + 1 x 2 + x + 1 ≥ 2 x 2 + 4 x + 5 - 2 m có nghiệm. Số phần tử của tập hợp S bằng
A. 20
B. 10
C. 15
D. 5
Gọi S là tập hợp các giá trị của tham số m để phương trình
1
9
x
-
m
1
3
x
+
2
m
+
1
0
có nghiệm. Tập RS có bao nhiêu giá trị nguyên? A. 4. B. 9. C. 0. D. 3.
Đọc tiếp
Gọi S là tập hợp các giá trị của tham số m để phương trình 1 9 x - m 1 3 x + 2 m + 1 = 0 có nghiệm. Tập R\S có bao nhiêu giá trị nguyên?
A. 4.
B. 9.
C. 0.
D. 3.
Gọi S là tập hợp các giá trị của tham số m để phương trình
1
9
x
−
m
1
3
x
+
2
m
+
1
0
có nghiệm. Tập
ℝ
S
có bao nhiêu giá trị nguyên? A. 4 B. 9 C. 0 D. 3
Đọc tiếp
Gọi S là tập hợp các giá trị của tham số m để phương trình 1 9 x − m 1 3 x + 2 m + 1 = 0 có nghiệm. Tập ℝ \ S có bao nhiêu giá trị nguyên?
A. 4
B. 9
C. 0
D. 3
Gọi S là tập hợp các giá trị thực của tham số m để phương trình
4
x
-
m
.
2
x
+
2
m
+
1
0
có nghiệm. Tập RS có bao nhiêu giá trị nguyên? A.1 B.4 C.9 D.7
Đọc tiếp
Gọi S là tập hợp các giá trị thực của tham số m để phương trình 4 x - m . 2 x + 2 m + 1 = 0 có nghiệm. Tập R\S có bao nhiêu giá trị nguyên?
A.1
B.4
C.9
D.7
Gọi S là tập hợp các giá trị thực của tham số m để phương trình 4 x – m . 2 x + 2 m + 1 = 0 có nghiệm. Tập R\S có bao nhiêu giá trị nguyên
A. 1
B. 4
C. 9
D. 7
