Tổng của cấp số nhân vô hạn: 1 3 ; - 1 9 ; 1 27 ; . . . . . ; - 1 n + 1 3 n ; . . . . là:
A. 1/4
B. 1/2
C. 3/4
D. 4
Tổng của cấp số nhân vô hạn 3 ; - 1 ; - 1 9 ; 1 27 ; . . . ; - 1 n + 1 3 n ; . . . l à
A. 1/4
B. 1/2
C. 9/4
D. 4
a. Có nhận xét gì về công bội của các cấp số nhân lùi vô hạn?
b. Cho ví dụ về một cấp số nhân lùi vô hạn và có công bội là số âm và một cấp số nhân lùi vô hạn có công bội là số dương và tính tổng của các cấp số nhân đó.
a) Cấp số nhân vô hạn với công bội q mà |q| < 1 là cấp số nhân lùi vô hạn
b) Ví dụ về cấp số nhân lùi vô hạn có công bội âm:
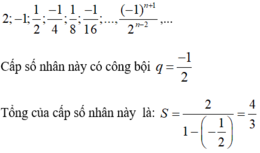

a) Có nhận xét gì về công bội của các cấp số nhân lùi vô hạn ?
b) Cho ví dụ về một cấp số nhân lùi vô hạn có công bội là số âm và một cấp số nhân lùi vô hạn có công bội là số dương và tính tổng của mỗi cấp số nhân đó ?
a) Tính tổng của cấp số nhân lùi vô hạn (un), với u1=\(\dfrac{2}{3}\),q=−\(\dfrac{1}{4}\)
b) Biểu diễn số thập phân vô hạn tuần hoàn 1,(6) dưới dạng phân số
a: \(S=\dfrac{\dfrac{2}{3}}{\dfrac{5}{4}}=\dfrac{8}{15}\)
b: 1,(6)=5/3
Cho cấp số nhân lùi vô hạn u n có công bội q. Khi đó tổng của cấp số nhân lùi vô hạn đó được tính bởi công thức nào sau đây:
A. S = 1 1 - q
B. S = u 1 1 - q
C. S = u 1 1 + q n
D. S = u 1 1 - q n
Đáp án B
- Cách giải:
Cho cấp số nhân lùi vô hạn
u
n
có công bội q. Khi đó tổng của cấp số nhân lùi vô hạn đó được tính bởi công thức 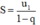
a) Tính tổng của cấp số nhân lùi vô hạn \(\left( {{u_n}} \right),\) với \({u_1} = \frac{2}{3},q = - \frac{1}{4}.\)
b) Biểu diễn số thập phân vô hạn tuần hoàn 1,(6) dưới dạng phân số.
a) \(S = \frac{{{u_1}}}{{1 - q}} = \frac{{\frac{2}{3}}}{{1 - \frac{{ - 1}}{4}}} = \frac{8}{{15}}\)
b) \(1,\left( 6 \right) = \frac{5}{3}\)
Tổng của cấp số nhân vô hạn : 1 2 , 1 6 , 1 18 , . . . , 1 2 . 3 n - 1 , . . . l à
A. 1/2
B. 3/8
C. 3/4
D. 3/2
Tính tổng của cấp số nhân lùi vô hạn: \(1 + \frac{1}{3} + {\left( {\frac{1}{3}} \right)^2} + ... + {\left( {\frac{1}{3}} \right)^n} + ...\).
Tổng trên là tổng của cấp số nhân lùi vô hạn có số hạng đầu \({u_1} = 1\) và công bội \(q = \frac{1}{3}\) nên
\(1 + \frac{1}{3} + {\left( {\frac{1}{3}} \right)^2} + ... + {\left( {\frac{1}{3}} \right)^n} + ... = \frac{1}{{1 - \frac{1}{3}}} = \frac{3}{2}\).
Tính tổng của cấp số nhân lùi vô hạn: 1 ; - 1 2 ; 1 4 ; - 1 8 ; . . . . ; - 1 2 n - 1 ; . . . . .
Tìm số hạng tổng quát của cấp số nhân lùi vô hạn có tổng bằng 3 và công bội q = 2/3