Cho y =f(x) là hàm số chẵn và liên tục trên R. Biết ∫ 0 1 f ( x ) d x = 1 2 ∫ 1 2 f ( x ) d x = 1 . Giá trị của ∫ - 2 2 f ( x ) 3 x + 1 bằng
A. 1.
B. 6.
C. 4.
D. 3.
Cho hàm số y = f(x) liên tục trên R và là hàm số chẵn, biết ∫ - 1 1 f ( x ) 1 + e x d x = 1 . Tính ∫ - 1 1 f ( x ) d x
A. 1
B. 2
C. 4
D. 1/2
Đáp án B
Phương pháp: Đặt t = - x
Cách giải: I = ∫ - 1 1 f ( x ) 1 + e x d x = 1 (1)
Đặt t = - x => dt = - dx
Đổi cận 
Khi đó:
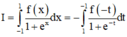
 (do là hàm chẵn)
(do là hàm chẵn)
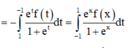
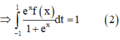
Từ (1), (2), suy ra
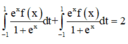
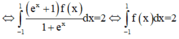
Cho hàm số y = f(x) liên tục trên R và là hàm số chẵn, biết ∫ - 1 1 f ( x ) 1 - e x d x = 1 tính ∫ - 1 1 f ( x ) d x
A. 1
B. 2
C. 4
D. 1/2
Cho y=f(x) là hàm số chẵn và liên tục trên R. Biết ∫ 0 1 f ( x ) d x = 1 2 f ( x ) d x = 1 . Giá trị của ∫ - 2 2 f ( x ) 3 x + 1 d x bằng
A. 1
B. 6
C. 4
D. 3
Cho hàm số y = f(x) xác định và liên tục trên R \ 0 biết x . f x ≠ - 1 ∀ x ≠ 0 f(1) = -2 và với ∀ x ∈ R \ 0 Tính ∫ 1 e f x d x
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho f(x) là hàm số chẵn, liên tục trên R thỏa mãn ∫ 0 1 f ( x ) d x = 2018 và g(x) là hàm số liên tục trên R thỏa mãn g ( x ) + g ( - x ) = 1 Tính tích phân I = ∫ - 1 1 f ( x ) . g ( x ) d x
A. I = 2018
B. I = 504,5
C. I =4036
D. I = 1008
Cho hàm số f(x) liên tục trên R và F(x) là một nguyên hàm của f(x), biết ∫ 0 9 f x d x = 9 và F(0) = 9.
A. F(9) = -3
B. F(9) = -12.
C. F(9) = 12.
D. F(9) = 6.
Cho hàm số f(x) liên tục trên R và F(x) là một nguyên hàm của f(x) biết ∫ 0 9 f x d x = 9 và F(0)=9
A. F(9) = -3
B. F(9) = -12
C. F(9) = 12
D. F(9) = 6
Cho hàm số y=f(x) liên tục, không âm trên R thỏa mãn f ( x ) . f ' ( x ) = 2 x f ( x ) 2 + 1 và f(0)=0. Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y=f(x) trên đoạn [1;3] lần lượt là:
A. M=20;m=2
B. M = 4 11 ; m = 3
C. M = 20 ; m = 2
D. M = 3 11 ; m = 3
Cho hàm số y = f (x) thỏa mãn f(0) = 1, f'(x) liên tục trên R và ∫ 0 3 f ' ( x ) dx = 9 .Giá trị của f(3) là
A. 6
B. 3
C. 10
D. 9