Phương trình sin 2 x = − 1 2 có bao nhiêu nghiệm thỏa 0 < x < π
A. 1
B. 3
C. 2
D. 4
Những câu hỏi liên quan
Phương trình
sin
2
x
-
1
2
có bao nhiêu nghiệm thỏa mãn
0
x
π
A. 1 B. 3 C. 2 D. 4
Đọc tiếp
Phương trình sin 2 x = - 1 2 có bao nhiêu nghiệm thỏa mãn 0 < x < π
A. 1
B. 3
C. 2
D. 4
Phương trình sin 2x + 3cos x 0 có bao nhiêu nghiệm trong khoảng
0
;
π
A. 0 B. 1 C. 2 D. 3
Đọc tiếp
Phương trình sin 2x + 3cos x =0 có bao nhiêu nghiệm trong khoảng 0 ; π
A. 0
B. 1
C. 2
D. 3
Trong các khoảng sau, m thuộc khoảng nào để phương trình sin^2 x-(2m+1) sin x.cos x + 2m cos^2 x = 0 có nghiệm thuộc khoảng (π/4 ; π/3)?
\(sin^2x-2m.sinx.cosx-sinx.cosx+2mcos^2x=0\)
\(\Leftrightarrow sinx\left(sinx-cosx\right)-2mcosx\left(sinx-cosx\right)=0\)
\(\Leftrightarrow\left(sinx-cosx\right)\left(sinx-2m.cosx\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}sinx=cosx\\sinx=2m.cosx\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}tanx=1\\tanx=2m\end{matrix}\right.\)
Do \(tanx=1\) ko có nghiệm đã cho nên \(tanx=2m\) phải có nghiệm trên khoảng đã cho
\(\Rightarrow tan\left(\dfrac{\pi}{4}\right)< 2m< tan\left(\dfrac{\pi}{3}\right)\)
\(\Rightarrow1< 2m< \sqrt[]{3}\)
\(\Rightarrow m\in\left(\dfrac{1}{2};\dfrac{\sqrt{3}}{2}\right)\) (hoặc có thể 1 đáp án là tập con của tập này cũng được)
Đúng 0
Bình luận (0)
Phương trình
-
x
2
+
3
x
-
2
.
s
i
n
[
π
(
4
x
2
+
2
x
)
]
0 có bao nhiêu nghiệm thực A. 5. B. 17. C. 13. D. 15.
Đọc tiếp
Phương trình - x 2 + 3 x - 2 . s i n [ π ( 4 x 2 + 2 x ) ] =0 có bao nhiêu nghiệm thực
A. 5.
B. 17.
C. 13.
D. 15.
Phương trình sin (2x +1) =-1/2 với x ϵ (0;π) có nghiệm là:
Lời giải:
$\sin (2x+1)=\frac{-1}{2}$
$\Rightarrow 2x+1=\frac{-\pi}{6}+2k\pi$ hoặc $2x+1=\frac{7}{6}\pi +2k\pi$ với $k$ nguyên
Với $2x+1=\frac{-\pi}{6}+2k\pi$
Do $x\in (0;\pi)$ nên $k=1$
$x=\frac{11}{12}\pi -\frac{1}{2}$
Với $2x+1=\frac{7\pi}{6}+2k\pi$
Do $x\in (0;\pi)$ nên $k=0$
$\Rightarrow x=\frac{7}{12}\pi -\frac{1}{2}$
Đúng 0
Bình luận (0)
Có bao nhiêu nghiệm của phương trình
sin
2
x
-
sin
x
0
thỏa mãn điều kiện
0
x
π
A. Đồ thị (III) xảy ra khi B. Đồ thị (IV) xảy ra khi C. Đồ thị (II) xảy ra khi D. Đồ thị (I) xảy ra khi
Đọc tiếp
Có bao nhiêu nghiệm của phương trình sin 2 x - sin x = 0 thỏa mãn điều kiện 0 < x < π
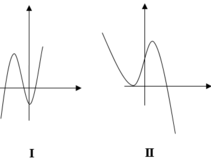
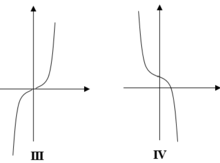
A. Đồ thị (III) xảy ra khi
B. Đồ thị (IV) xảy ra khi
C. Đồ thị (II) xảy ra khi
D. Đồ thị (I) xảy ra khi
Số nghiệm thuộc
(
0
;
π
)
của phương trình
sin
x
+
1
+
c
o
s
2
x
2
(
c
o
s
3
3
x
+
1
)
là A. 1 B. 2 C. 3 D. 4
Đọc tiếp
Số nghiệm thuộc ( 0 ; π ) của phương trình sin x + 1 + c o s 2 x = 2 ( c o s 3 3 x + 1 ) là
A. 1
B. 2
C. 3
D. 4
Phương trình
sin
2
x
-
2
2
có bao nhiêu nghiệm thuộc khoảng
0
,
π
? A. 4 B. 3 C. 2 D. 1
Đọc tiếp
Phương trình sin 2 x = - 2 2 có bao nhiêu nghiệm thuộc khoảng 0 , π ?
A. 4
B. 3
C. 2
D. 1
Tìm tất cả giá trị của m để phương trình:
cos 2x + (2m - 3) sin x + m - 2 = 0 có đúng 2 nghiệm phân biệt x thuộc [-π/2 ; π/2]
Xem chi tiết
\(\Leftrightarrow1-2sin^2x+\left(2m-3\right)sinx+m-2=0\)
\(\Leftrightarrow2sin^2x-\left(2m-3\right)sinx-m+1=0\)
\(\Leftrightarrow2sin^2x+sinx-2\left(m-1\right)sinx-\left(m-1\right)=0\)
\(\Leftrightarrow sinx\left(2sinx+1\right)-\left(m-1\right)\left(2sinx+1\right)=0\)
\(\Leftrightarrow\left(2sinx+1\right)\left(sinx-m+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=-\dfrac{1}{2}\\sinx=m-1\end{matrix}\right.\)
Pt có đúng 2 nghiệm thuộc khoảng đã cho khi và chỉ khi:
\(\left\{{}\begin{matrix}m-1\ne-\dfrac{1}{2}\\-1\le m-1\le1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m\ne\dfrac{1}{2}\\0\le m\le2\end{matrix}\right.\)
Đúng 2
Bình luận (0)