Tích phân I = ∫ π 4 π 3 d x sin 2 x bằng
A. cot π 3 − cot π 4
B. cot π 3 + cot π 4
C. − cot π 3 + cot π 4
D. − cot π 3 − cot π 4
Những câu hỏi liên quan
Tính:F=Cos(π/4+α) x cos(π/4-α)
G=Sin(π/3+α) x cos(π/3-α)
H=cos(π/2-α) x sin(π/2+α)
I=sin(π/4+α) - cos(π/4-α)
K=cos(π/6-x) - sin(π/3+x)
Cho hàm số yf(x) liên tục trên đoạn [0;π/3].Biết f’(x).cosx+f(x).sinx1, x ϵ [0;π/3] và f(0)1. Tính tích phân
I
∫
0
π
3
f
x
d
x
A. 1/2 + π/3 B.
3
+
1
2
C. ...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên đoạn [0;π/3].Biết f’(x).cosx+f(x).sinx=1, x ϵ [0;π/3] và f(0)=1. Tính tích phân I = ∫ 0 π 3 f x d x
A. 1/2 + π/3
B. 3 + 1 2
C. 3 - 1 2
D. 1/2
Diện tích của hình phẳng được giới hạn bởi các đường: y = tanx; y = 0; x = -π/4 và x = π/4 bằng:
A. π; B. -π;
C. ln2; D. 0
Đáp án: C.
Hướng dẫn: Diện tích được tính bởi tích phân
Đúng 0
Bình luận (0)
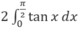
Diện tích của hình phẳng được giới hạn bởi các đường: y = tanx; y = 0; x = - π /4 và x = π /4 bằng:
A. π ; B. - π ;
C. ln2; D. 0
Đáp án: C.
Hướng dẫn: Diện tích được tính bởi tích phân
Đúng 0
Bình luận (0)
Cho khối trụ có bán kính đáy bằng a và thiết diện đi qua là một hình vuông. Thể tích khối trụ là:A. 2
π
a
3
B. 2
π
a
3
/3C. 4
π
a
3
D.
π
a
3
Đọc tiếp
Cho khối trụ có bán kính đáy bằng a và thiết diện đi qua là một hình vuông. Thể tích khối trụ là:
A. 2 π a 3 B. 2 π a 3 /3
C. 4 π a 3 D. π a 3
Chọn A.
Thiết diện qua trục của hình trụ là hình vuông nê hình trụ có bán kính đáy là a, chiều cao là 2a.
Do đó thể tích khối trụ là:
V = πR 2 h = 2 πa 3
Đúng 0
Bình luận (0)
Tích phân I = ∫ 0 α x sin x d x với α ∈ [0; π] là:
A. αcosα - sinα
B. αcosα + sinα
C. -αcosα + sinα
D. -αcosα - sinα
Chọn C
Áp dụng công thức tích phân từng phần ta có:
Đúng 0
Bình luận (0)
Hình bên minh họa : hình gồm một nửa hình cầu và một hình nón.Thể tích của hình nhận giá trị nào sau đây?A. (2/3).
π
x
3
(
c
m
3
)B.
π
.x3
x
3
(
c
m
3
)C. (4/3).
π
....
Đọc tiếp
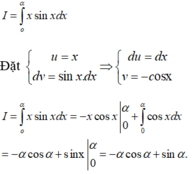
Hình bên minh họa : hình gồm một nửa hình cầu và một hình nón.Thể tích của hình nhận giá trị nào sau đây?
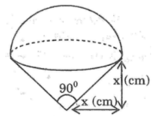
A. (2/3). π x 3 ( c m 3 )
B. π .x3 x 3 ( c m 3 )
C. (4/3). π . x 3 ( c m 3 )
D. 2 π . x 3 ( c m 3 )
Thể tích nửa hình cầu là: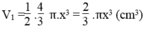 
Thể tích hình nón là :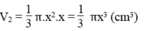 
Tổng thể tích của hai hình: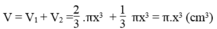 
Vậy chọn đáp án B
Đúng 0
Bình luận (0)
Một hình nón có đường kính đáy là 2a
π
3, góc ở đỉnh 120
°
. Thể tích của khối nón đó theo a là:A. 2
3
π
a
3
B. 3
π
a
3
C.
π
a
3
D.
π...
Đọc tiếp
Một hình nón có đường kính đáy là 2a π 3, góc ở đỉnh 120 ° . Thể tích của khối nón đó theo a là:
A. 2 3 π a 3 B. 3 π a 3
C. π a 3 D. π a 3 3
Chọn C.
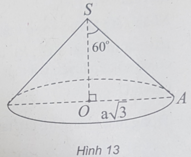
(h.13) Gọi S là đỉnh hình nón, O là tâm đáy, A là một điểm thuộc đường tròn đáy.
Theo giả thiết, đường tròn đáy có bán kính R = OA = a 3 và ∠ = 60 °
Trong tam giác SOA vuông tại O, ta có: OA = SO.tan60 ° ⇒ SO = a.
Do đó chiều cao của hình nón là h = a.
Vậy thể tích hình nón là: V = π a 3
Đúng 0
Bình luận (0)
Đặt điện áp xoay chiều u 100
2
cos100πt (V) vào hai đầu một tụ điện có điện dung 2.
10
-
4
/
π
(F).Biểu thức cường độ dòng điện qua tụ điện là :A. i 2cos(100
π
t -
π
/2) (A).B. i 2
2
cos(100
π
t + ...
Đọc tiếp
Đặt điện áp xoay chiều u = 100 2 cos100πt (V) vào hai đầu một tụ điện có điện dung 2. 10 - 4 / π (F).
Biểu thức cường độ dòng điện qua tụ điện là :
A. i = 2cos(100 π t - π /2) (A).
B. i = 2 2 cos(100 π t + π /2) (A).
C. i = 2cos(100 π t + π /2) (A).
D. i = 2 2 cos(100 π t - π /2) (A).
tính tích phân của tanx.dx cận từ π/4 đến -π/4
ai giúp mình với. mình đang gấp ạ
Lâu ko ôn lại cũng hơi miss tích phân r :v
\(\int\limits^{\dfrac{-\pi}{4}}_{\dfrac{\pi}{4}}\tan x.dx\)
\(\int\tan x.dx=\int\dfrac{\sin x}{\cos x}.dx=-\int\dfrac{1}{\cos x}.d\left(\cos x\right)=-ln\left|\cos x\right|\)
\(\Rightarrow\int\limits^{\dfrac{-\pi}{4}}_{\dfrac{\pi}{4}}\tan x.dx=-ln\left|\cos\dfrac{-\pi}{4}\right|+ln\left|\cos\dfrac{\pi}{4}\right|\)
Đúng 1
Bình luận (0)