Vì hs y = (m-1)x +m +3 đi qua điểm (1; -4) nên ta đc :

-4 = (m-1) + m+3

<=> -4 = 2m + 2

<=> m =-3

1) Đặt tên cho dễ giải nè:

(d1) : y= (m-1) x + m+ 3

(d2) : y = -2x + 1

(d1) // (d2) <=> m - 1 = -2 và m+ 3 \(\ne\)1

<=> m = -1 và m \(\ne\)-2 

1. để đồ thị của hàm số \(y=\left(m-1\right)x+m+3\) // với \(y=-2x+1\),

\(\left\{{}\begin{matrix}m-1=-2\\m+3\ne1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=-1\\m\ne-2\end{matrix}\right.\)

2. để đi qua điểm (1;-4),

\(-4=m-1+m+3\\ \Leftrightarrow-4=2m+2\Leftrightarrow m=-3\)

3. \(y=\left(m-1\right)x+m+3\\ \Leftrightarrow x+y=mx+m+3\\ \Leftrightarrow x+y-3=m\left(x+1\right)\)

tọa độ điểm cố định là nghiệm của hpt

\(\left\{{}\begin{matrix}x+y-3=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=4\end{matrix}\right.\)

đ cđịnh M(-1;4)

4. \(y=\left(m-1\right)x+m+3\)

+ Khi x=0, y=m+3

+ khi y=0, \(x=\dfrac{-m-3}{m-1}\)

Để \(S=1\Rightarrow\dfrac{-m-3}{m-1}.\left(m+3\right)=2\\ \Leftrightarrow\left(m+3\right)^2=2\left(1-m\right)\\ \Leftrightarrow m^2+8m+7=0\Leftrightarrow\left(m+1\right)\left(m+7\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-7\end{matrix}\right.\)

a.

ĐTHS song với với đường thẳng đã cho khi:

\(\left\{{}\begin{matrix}m-2=-1\\m+3\ne3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m=1\\m\ne0\end{matrix}\right.\) \(\Rightarrow m=1\)

b.

Gọi A là giao điểm của ĐTHS và \(y=2x+4\Rightarrow y_A=2\)

\(\Rightarrow2x_A+4=2\Rightarrow x_A=-1\)

\(\Rightarrow A\left(-1;2\right)\)

Thế tọa độ A vào (1):

\(-1\left(m-2\right)+m+3=2\Leftrightarrow5=2\left(ktm\right)\)

Vậy ko tồn tại m thỏa mãn yêu cầu đề bài

a. \(\left\{{}\begin{matrix}DB:m+4>0\Leftrightarrow m>-4\\NB:m+4< 0\Leftrightarrow m< -4\end{matrix}\right.\)

\(a,\) Đồng biến \(\Leftrightarrow m+4>0\Leftrightarrow m>-4\)

Nghịch biến \(m+4< 0\Leftrightarrow m< -4\)

\(b,A\left(-1;2\right)\in\left(d\right)\Leftrightarrow-m-4-m+6=2\Leftrightarrow m=0\)

\(\Leftrightarrow y=4x+6\)

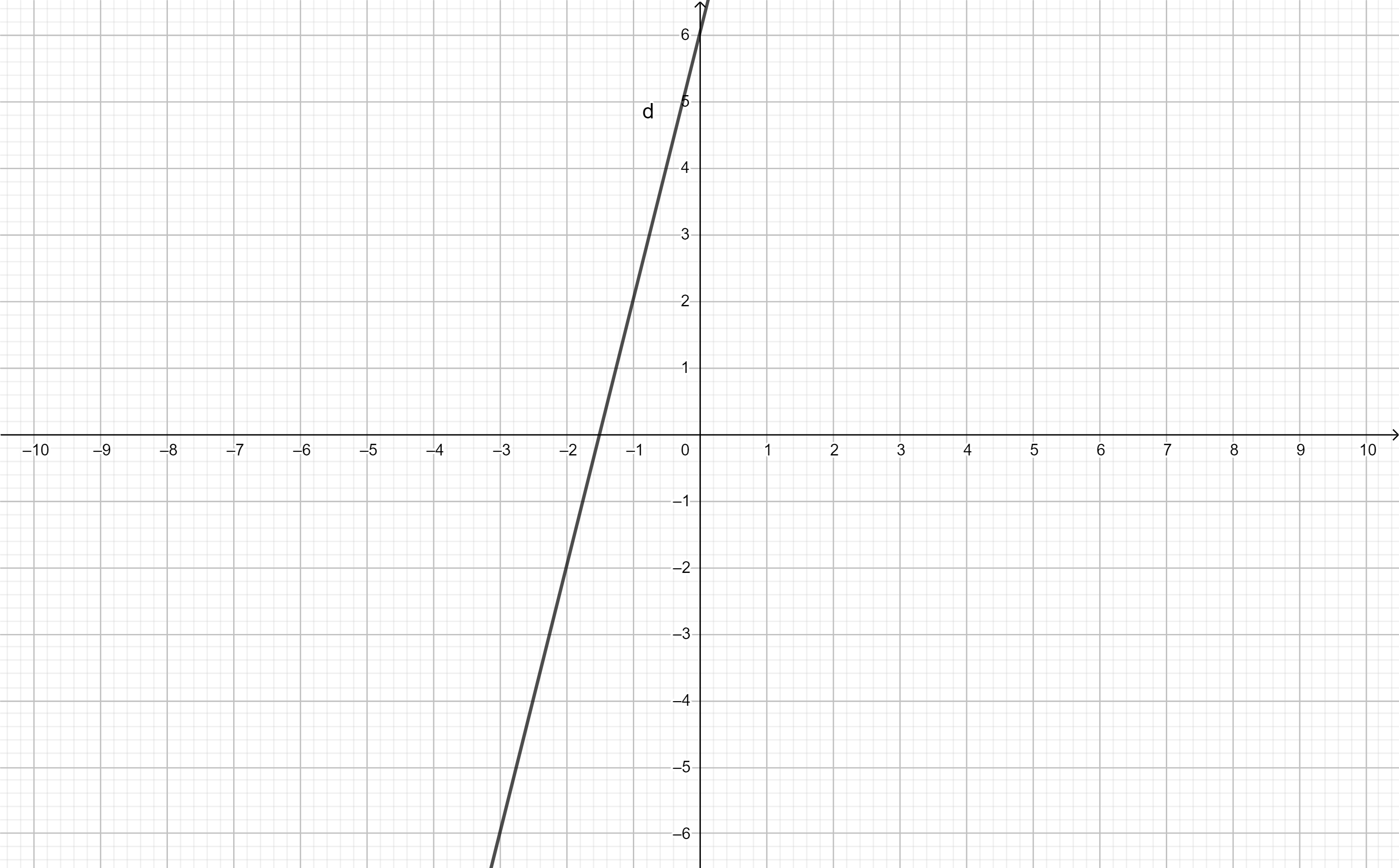
gọi hs y=(m+4)x-m+6 là (d)
hàm số (d) đồng biến <=> a>0
<=> m+4>0
<=> m>-4
vậy m>-4 thì (d) đồng biến 
hàm số (d) nghịch biến <=> a<0
<=> m+4<0
<=> m<-4
vậy m<-4 thì (d) nghịch biến

3.

\(y'=\dfrac{3m-1}{\left(x+3m\right)^2}\)

Hàm nghịch biến trên khoảng đã cho khi:

\(\left\{{}\begin{matrix}3m-1< 0\\-3m\le6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< \dfrac{1}{3}\\m\ge-2\end{matrix}\right.\)

\(\Rightarrow-2\le m< \dfrac{1}{3}\Rightarrow m=\left\{-2;-1;0\right\}\)

4.

\(y'=\dfrac{3m-2}{\left(x+3m\right)^2}\)

Hàm đồng biến trên khoảng đã cho khi:

\(\left\{{}\begin{matrix}3m-2>0\\-3m\ge-6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>\dfrac{2}{3}\\m\le2\end{matrix}\right.\)

\(\Rightarrow\dfrac{2}{3}< m\le2\Rightarrow m=\left\{1;2\right\}\)

a) Hàm số đồng biến trên R\(\Rightarrow a>0\Rightarrow m-2>0\Rightarrow m>2\)

b) Hàm số nghịch biến trên R

    \(\Leftrightarrow a< 0\Rightarrow m-2< 0\Rightarrow m< 2\)