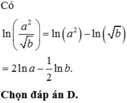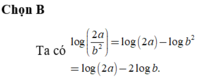Tính (a + b)(a + b)2 (với a, b là hai số tùy ý).

Những câu hỏi liên quan
Tính [a + (-b)]3 (với a, b là hai số tùy ý).
Áp dụng hằng đẳng thức (4) ta có:
[a + (-b)]3 = a3 + 3a2 (-b) + 3a(-b)2 + (-b)3
= a3 - 3a2b + 3ab2 - b3
Đúng 0
Bình luận (0)
Tính (a - b)(a2 + ab + b2 ) (với a, b là hai số tùy ý).
(a - b)(a2 + ab + b2 ) = a(a2 + ab + b2 ) - b(a2 + ab + b2 )
= a3 + a2 b + ab2 - ba2 - ab2 - b3
= a3 - b3
Đúng 0
Bình luận (0)
Tính (a + b)(a2 – ab + b2) (với a, b là hai số tùy ý).
(a + b)(a2 – ab + b2 ) = a(a2 – ab + b2 ) + b(a2 – ab + b2 )
= a3 – a2b + ab2 + ba2 – ab2 + b3
= a3 + b3
Đúng 0
Bình luận (0)
Tính [a + (-b)]2 (với a, b là các số tùy ý).
Áp dụng hằng đẳng thức (1) ta có:
[a + (-b)]2 = a2 + 2.a.(-b) + (-b)2 = a2 - 2ab + b2
Đúng 0
Bình luận (0)
Thực hiện phép tính (a + b)(a – b) (với a, b là các số tùy ý).
(a + b)(a – b) = a(a – b) + b(a – b)
= a2 - ab + ba - b2
= a2 - b2
Đúng 0
Bình luận (0)
Với a và b là hai số thực dương tùy ý,
log
a
2
b
3
bằng A.
1
2
log
a
+
1
3
log
b
B. 2loga +lobgb C. 2loga+3logb D. 2loga.3logb
Đọc tiếp
Với a và b là hai số thực dương tùy ý, log a 2 b 3 bằng
A. 1 2 log a + 1 3 log b
B. 2loga +lobgb
C. 2loga+3logb
D. 2loga.3logb
Ta có: log a 2 b 3 = log a 2 + log b 3
= 2 log a + 3 log b a , b > 0
Chọn đáp án C.
Đúng 0
Bình luận (0)
Với a và b là hai số thực dương tùy ý,
log
a
2
b
3
bằng A.
1
2
log
a
+
1
3
log
b
B.
2
log...
Đọc tiếp
Với a và b là hai số thực dương tùy ý, log a 2 b 3 bằng
A. 1 2 log a + 1 3 log b
B. 2 log a + log b
C. 2 log a + 3 log b
D. 2 log a . 3 log b
Với a, b là hai số thực dương tùy ý,
ln
a
2
b
bằng A.
2
log
a
-
1
2
log
b
B.
2
log
a
+
1
2
log...
Đọc tiếp
Với a, b là hai số thực dương tùy ý, ln a 2 b bằng
A. 2 log a - 1 2 log b
B. 2 log a + 1 2 log b
C. 2 ln a ln b
D. 2 ln a - 1 2 ln b
Với a,b là hai số dương khác không tùy ý,
log
2
a
b
2
bằng. A.
2
log
a
-
log
b
B.
log
(
2
a
)
-
2
log
b
C.
log...
Đọc tiếp
Với a,b là hai số dương khác không tùy ý, log 2 a b 2 bằng.
A. 2 log a - log b
B. log ( 2 a ) - 2 log b
C. log a log b
D. log ( 2 a ) 2 log b