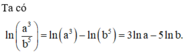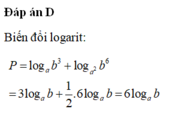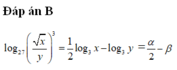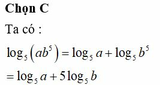Thực hiện phép tính (a + b)(a – b) (với a, b là các số tùy ý).

Những câu hỏi liên quan
với a,b,c là các số thực dương tùy ý
Đặt \(\left\{{}\begin{matrix}\sqrt{a-1}=x\\\sqrt{b-1}=y\\\sqrt{c-1}=z\end{matrix}\right.\) thì BĐT cần chứng minh trở thành:
\(\sqrt{\left(x^2+1\right)\left(y^2+1\right)\left(z^2+1\right)+z^2+1}\ge x+y+z\)
\(\Leftrightarrow\left(x^2+1\right)\left(y^2+1\right)\left(z^2+1\right)+z^2+1\ge\left(x+y+z\right)^2\)
\(\Leftrightarrow x^2y^2z^2+x^2y^2+y^2z^2+z^2x^2-2xy-2yz-2zx+z^2+2\ge0\)
\(\Leftrightarrow\left(x^2y^2z^2+z^2-2xyz^2\right)+\left(x^2z^2+y^2z^2+2xyz^2\right)-2z\left(x+y\right)+1+\left(x^2y^2-2xy+1\right)\ge0\)
\(\Leftrightarrow\left(xyz-z\right)^2+\left(xz+yz\right)^2-2\left(xz+yz\right)+1+\left(xy-1\right)^2\ge0\)
\(\Leftrightarrow\left(xyz-z\right)^2+\left(xz+yz-1\right)^2+\left(xy-1\right)^2\ge0\) (luôn đúng)
Đúng 2
Bình luận (0)
Tính [a + (-b)]2 (với a, b là các số tùy ý).
Áp dụng hằng đẳng thức (1) ta có:
[a + (-b)]2 = a2 + 2.a.(-b) + (-b)2 = a2 - 2ab + b2
Đúng 0
Bình luận (0)
Với các số thực dụng a và b tùy ý,
ln
a
3
b
5
bằng A.
3
5
ln
a
b
B.
3
ln
a
5
ln
b
C.
3
ln
...
Đọc tiếp
Với các số thực dụng a và b tùy ý, ln a 3 b 5 bằng
A. 3 5 ln a b
B. 3 ln a 5 ln b
C. 3 ln a + 5 ln b
D. 3 ln a - 5 ln b
a) Thực hiện các phép tính sau:
1,2.2,5; 125:0,25.
b) Thực hiện lại các phép tính ở câu a bằng cách đưa về phép tính với phân số thập phân.
a) 1,2.2,5 = 3;
125 : 0,25 = 500
b)
\(1,2.2,5 = \dfrac{6}{5}.\dfrac{5}{2} = \dfrac{{30}}{{10}} = 3\)
\(125:0,25 = 125:\dfrac{1}{4} = 125.4 = 500\)
Đúng 0
Bình luận (0)
Với a, b là các số thực dương tùy ý và a khác 1, đặt
P
log
a
b
3
+
log
a
2
b
6
Mệnh đề nào dưới đây đúng ? A.
P
9
log
a
b
B. P 27...
Đọc tiếp
Với a, b là các số thực dương tùy ý và a khác 1, đặt P = log a b 3 + log a 2 b 6 Mệnh đề nào dưới đây đúng ?
A. P = 9 log a b
B. P = 27 log a b 15
C. P = 15 log a b
D. P = 6 log a b
Với a, b là các số thực dương tùy ý và a khác 1, đặt
P
log
a
b
3
+
log
a
2
b
6
.
Mệnh đề nào dưới đây đúng? A.
P
9
log
a
b
B.
P
27
log
a
b...
Đọc tiếp
Với a, b là các số thực dương tùy ý và a khác 1, đặt P = log a b 3 + log a 2 b 6 . Mệnh đề nào dưới đây đúng?
A. P = 9 log a b
B. P = 27 log a b
C. P = 15 log a b
D. P = 6 log a b
Đáp án D
P = log a b 3 + log a 2 b 6 = 3 log a b + 3 log a b = 6 log a b
Đúng 0
Bình luận (0)
Với các số thực dương x,y tùy ý , đặt
log
3
x
a
,
log
3
y
b
. Mệnh đề nào dưới đây là đúng ?
Đọc tiếp
Với các số thực dương x,y tùy ý , đặt log 3 x = a , log 3 y = b . Mệnh đề nào dưới đây là đúng ?
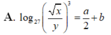
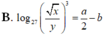
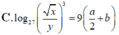
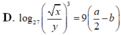
Với a,b là số thực dương tùy ý,
log
5
a
b
5
bằng A.
5
log
5
a
+
log
5
b
B.
log
5
a
+
1
5...
Đọc tiếp
Với a,b là số thực dương tùy ý, log 5 a b 5 bằng
A. 5 log 5 a + log 5 b
B. log 5 a + 1 5 log 5 b
C. log 5 a + 5 log 5 b
D. 5 log 5 a + log 5 b
Tính (a + b)(a + b)2 (với a, b là hai số tùy ý).
a + b)(a + b)2 = (a + b)(a2 + 2ab + b2 )
= a(a2 + 2ab + b2 ) + b(a2 + 2ab + b2 )
= a3 + 2a2 b + ab2 + ba2 + 2ab2 + b3
= a3 + 3a2 b + 3ab2 + b3
Đúng 0
Bình luận (0)