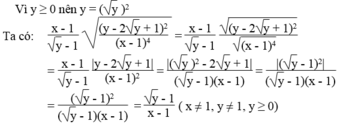Rút gọn các phân thức: 14 x y 5 2 x - 3 y 21 x 2 y 2 x - 3 y 2

Những câu hỏi liên quan
1.Rút gọn biểu thức `P=(x+4)^2+(x+5)(x-5)-2x(x+1)`
2.Tính giá trị biểu thức `Q=xy-4y-5x+20 với x=14;y=5,5`
\(P=x^2+8x+16+x^2-25-2x^2-2x=6x-9\\ Q=y\left(x-4\right)-5\left(x-4\right)=\left(y-5\right)\left(x-4\right)\\ Q=\left(5,5-5\right)\left(14-4\right)=0,5\cdot10=5\)
Đúng 2
Bình luận (0)
Câu 14: Kết quả phân tích đa thức 5x3 - 10x2y + 5xy2 thành nhân tử là:A. 5x(x – y)2 B. x(5x – y)2 C. -5x(x + y)2 D. x(x + 5y)2 Câu 15: Rút gọn phân thức:dfrac{15xleft(3-yright)}{45xleft(y-3right)}ta được kết quả là:A. 3 B. -3x C.dfrac{1}{3x} D.dfrac{-1}{3}
Đọc tiếp
Câu 14: Kết quả phân tích đa thức 5x3 - 10x2y + 5xy2 thành nhân tử là:
A. 5x(x – y)2 B. x(5x – y)2 C. -5x(x + y)2 D. x(x + 5y)2
Câu 15: Rút gọn phân thức:\(\dfrac{15x\left(3-y\right)}{45x\left(y-3\right)}\)ta được kết quả là:
A. 3 B. -3x C.\(\dfrac{1}{3x}\) D.\(\dfrac{-1}{3}\)
Rút gọn các biểu thức:
x
-
1
y
-
1
y
-
2
y
+
1
2...
Đọc tiếp
Rút gọn các biểu thức: x - 1 y - 1 y - 2 y + 1 2 x - 1 4 x ≠ 1 , y ≠ 1 , y ≥ 0
Bài 4 (3,0 điểm) Rút gọn các phân thức sau: B = (x + y)² - z²/x + y + z
c) C = x² - 6x + 5/x² - 2x + 1
b: \(B=\dfrac{\left(x+y\right)^2-z^2}{x+y+z}\)
\(=\dfrac{\left(x+y-z\right)\left(x+y+z\right)}{x+y+z}\)
=x+y-z
c:
ĐKXĐ: x<>1
\(C=\dfrac{x^2-6x+5}{x^2-2x+1}\)
\(=\dfrac{\left(x-1\right)\left(x-5\right)}{\left(x-1\right)^2}\)
\(=\dfrac{x-5}{x-1}\)
Đúng 0
Bình luận (0)
x^5+x^4-16x-16/x^3-6x^2-9x+14
a)Tìm điều kiện của x để giá trị các phân thức được xác định
b)Rút gọn phân thức
c)Tìm giá trị của x để giá trị của phân thức bằng 0
d)Tìm giá trị của phân thức A tại x=3
Cho xy/x^2+y^=5/8. Rút gọn phân thức P= x^2-2xy+y^2/x^2+2xy+y^2
1. Rút gọn phân thức \(\dfrac{\left(x+y\right)^2}{x^2-y^2}=\) ta được kết quả là:
2. Rút gọn phân thức \(\dfrac{x^2-3x}{x^2-9}=\)
giúp mình với nhé mình đang cần gấp ạ
1. = \(\dfrac{x+y}{x-y}\)
2. = \(\dfrac{x}{x+3}\)
Đúng 0
Bình luận (0)
Rút gọn các phân thức: \(\dfrac{x^3-y^3+z^3+3xyz}{\left(x+y\right)^2+\left(y+z\right)^2+\left(z-x\right)^2}\)
Rút gọn các phân thức sau:
b) x^3-x^2y+xy^2/x^3+y^3
c) (2x^2+2x)(x-2)^2/(x^3-4x)(x+1)
\(b,=\dfrac{x\left(x^2-xy+y^2\right)}{\left(x+y\right)\left(x^2-xy+y^2\right)}=\dfrac{x}{x+y}\left(x\ne-y\right)\\ c,=\dfrac{2x\left(x+1\right)\left(x-2\right)^2}{x\left(x-2\right)\left(x+2\right)\left(x+1\right)}=\dfrac{2\left(x-2\right)}{x+2}\left(x\ne-1;x\ne\pm2;x\ne0\right)\)
Đúng 2
Bình luận (0)
b: \(\dfrac{x^3-x^2y+xy^2}{x^3+y^3}=\dfrac{x\left(x^2-xy+y^2\right)}{\left(x+y\right)\left(x^2-xy+y^2\right)}=\dfrac{x}{x+y}\)
c: \(\dfrac{\left(2x^2+2x\right)\left(x-2\right)^2}{\left(x^3-4x\right)\left(x+1\right)}=\dfrac{2x\left(x+1\right)\left(x-2\right)^2}{x\left(x-2\right)\left(x+2\right)\left(x+1\right)}=\dfrac{2\left(x-2\right)}{x+2}\)
Đúng 0
Bình luận (0)
Rút gọn các biểu thức đại số sau:
a) \(6(y - x) - 2(x - y)\)
b) \(3{x^2} + x - 4x - 5{x^2}\)
a) Cách 1:
\(6(y - x) - 2(x - y)\)
\( = 6y - 6x - 2x + 2y\)
\( = 8y - 8x\)
Cách 2:
\(6(y - x) - 2(x - y)\\= 6(y-x)+2(y-x)\\=(6+2).(y-x)\\=8.(y-x)\\=8y-8x\)
b) \(3{x^2} + x - 4x - 5{x^2}\)
\( = (3{x^2} - 5{x^2}) + (x - 4x)\)
\( = - 2{x^2} - 3x\)
Đúng 0
Bình luận (0)