Lập phương trình tham số của đường thẳng d đi qua điểm M 0 x 0 , y 0 , z 0 và vuông góc với mặt phẳng (P): Ax + By + Cz + D = 0.

Những câu hỏi liên quan
Trong mặt phẳng tọa độ cho hai điểm A(3;0), B(0;2) và đường thẳng d: x + y 0.a) Lập phương trình tham số của đường thẳng Δ đi qua A và song song với db) Lập phương trình đường tròn đi qua A,B và có tâm thuộc đường thẳng dc) Lập phương trình chính tắc của elip đi qua điểm B và có tâm sai
e
5
3
Đọc tiếp
Trong mặt phẳng tọa độ cho hai điểm A(3;0), B(0;2) và đường thẳng d: x + y = 0.
a) Lập phương trình tham số của đường thẳng Δ đi qua A và song song với d
b) Lập phương trình đường tròn đi qua A,B và có tâm thuộc đường thẳng d
c) Lập phương trình chính tắc của elip đi qua điểm B và có tâm sai e = 5 3
Đường thẳng Δ song song với d ⇒ Δ: x + y + c = 0, (c ≠ 0)
Vì Δ đi qua A ⇒ 3 + 0 + c = 0 ⇒ c = -3(tm)
Vậy đường thẳng Δ có dạng: x+y-3=0
Vì đường tròn có tâm I thuộc d nên I(a;-a)
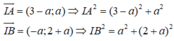
Vì đường tròn đi qua A, B nên I A 2 = I B 2 ⇒ (3 - a ) 2 + a 2 = a 2 + (2 + a ) 2 ⇔ (3 - a ) 2 = (2 + a ) 2
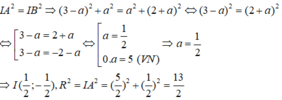
Vậy phương trình đường tròn có dạng:
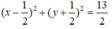
Ta có:
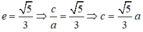
Giả sử elip (E) có dạng:
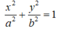
Vì (E) đi qua B nên:
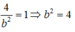
Mà
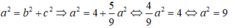
Vậy phương trình chính tắc của elip (E) là:
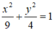
Đúng 0
Bình luận (0)
Lập phương trình tham số của đường thẳng \(\Delta \) đi qua điểm \(M\left( { - 1;2} \right)\) và song song với đường thẳng \(d:3x - 4y - 1 = 0\).
Vì hai đường thẳng \(\Delta \) và d song song với nhau nên ta có thể chọn \(\overrightarrow {{n_\Delta }} = \overrightarrow {{n_d}} = \left( {3; - 4} \right)\).
Mặt khác, \(\Delta \) đi qua điểm \(M\left( { - 1;2} \right)\)nên phương trình \(\Delta \) là:
\(3\left( {x + 1} \right) - 4\left( {y - 2} \right) = 0 \Leftrightarrow 3x - 4y + 11 = 0\).
Đúng 0
Bình luận (0)
Phương trình tham số của đường thẳng (d) đi qua điểm M( 2; -5) và vuông góc với đường thẳng (d’) : x+ 6y -7 0 là: D.Tất cả sai
Đọc tiếp
Phương trình tham số của đường thẳng (d) đi qua điểm M( 2; -5) và vuông góc với đường thẳng (d’) : x+ 6y -7= 0 là:
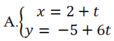
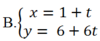
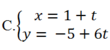
D.Tất cả sai
Đáp án A
Do 2 đường thẳng d và (d’) vuông góc với nhau nên VTCP của đường thẳng này là VTPT của đường thẳng kia và ngược lại.
Mà đường thẳng (d’) có VTPT là n → ( 1 ; 6 ) n ê n u → ( 1 ; 6 ) là VTCP của đường thẳng (d) .
Khi đó phương trình tham số của đường thẳng (d) cần tìm là:
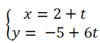
Đúng 1
Bình luận (0)
Trong không gian Oxyz, lập phương trình tham số của đường thẳng d đi qua điểm M(2;-1;1), vuông góc với đường thẳng và song song với mặt phẳng (P): 2x - 3y + z - 2 0. A.
d
:
x
-
2
4
y
+
1
5...
Đọc tiếp
Trong không gian Oxyz, lập phương trình tham số của đường thẳng d đi qua điểm M(2;-1;1), vuông góc với đường thẳng
 và song song với mặt phẳng (P): 2x - 3y + z - 2 = 0.
và song song với mặt phẳng (P): 2x - 3y + z - 2 = 0.
A. d : x - 2 4 = y + 1 5 = z - 1 7
B. d: x = 2 + 4t, y = 1 + 5t, z = 1 + 7t
C. d: x = 2 +4t, y = -1 - 5t, z = 1 + 7t
D. d: x = -2 + 4t, y = 1 + 5t, z = -1 + 7t
Đáp án B
Từ giả thiết suy ra
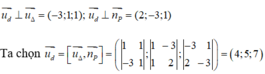
Mặt khác đường thẳng d đi qua điểm M(2;-1;1) nên phương trình tham số của đường thẳng d là: x = 2+ 4t, y = -1, + 5t, z = 1 + 7t.
Vậy đáp án đúng là B.
Đúng 0
Bình luận (0)
Lập phương trình tham số của đường thẳng:
Đi qua hai điểm A(1 ; 0 ; -3) và B(3 ; -1 ; 0).
Đường thẳng AB nhận 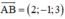 là 1 vtcp và đi qua A(1; 0; -3)
là 1 vtcp và đi qua A(1; 0; -3)
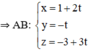
Đúng 0
Bình luận (0)
Trong không gian Oxyz, lập phương trình tham số của đường thẳng d đi qua điểm A(-2;3;1), vuông góc với trục Ox, đông thời d song song với mặt phẳng: (P): x + 2y - 3z 0 A. d: x 2, y -3 + 3t, z -1 + 2t B. d: x -2, y 3 - 3t, z 1 + 2t C. d: x -2, y 3 + 3t, z 1 + 2t D. Đáp án khác
Đọc tiếp
Trong không gian Oxyz, lập phương trình tham số của đường thẳng d đi qua điểm A(-2;3;1), vuông góc với trục Ox, đông thời d song song với mặt phẳng: (P): x + 2y - 3z = 0
A. d: x = 2, y = -3 + 3t, z = -1 + 2t
B. d: x = -2, y = 3 - 3t, z = 1 + 2t
C. d: x = -2, y = 3 + 3t, z = 1 + 2t
D. Đáp án khác
Lập phương trình tham số của đường thẳng d đi qua điểm
M
0
x
0
,
y
0
,
z
0
và song song với hai mặt phẳng cắt nhau(P) Ax + By + Cz + D 0...
Đọc tiếp
Lập phương trình tham số của đường thẳng d đi qua điểm M 0 x 0 , y 0 , z 0 và song song với hai mặt phẳng cắt nhau
(P) Ax + By + Cz + D = 0 và (Q): A’x + B’y + C’z + D’ = 0
Do (P) và (Q) cắt nhau nên n P → ∧ n Q → ≠ 0 → . Đường thẳng d đi qua M 0 và có vecto chỉ phương
![]()
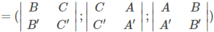
Do đó phương trình tham số của d là:
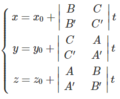
Đặc biệt phương trình trên cũng là phương trình đường thẳng là giao của hai mặt phẳng cắt nhau (P): Ax + By + Cz + D = 0 và (Q): A’x + B’y + C’z + D’ = 0 với M 0 là điểm chung của (P) và (Q).
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho điểm M (2 ; 1 ; 0) và đường thẳng
∆
:
x
-
1
2
y
+
1
1
z
-
1
. Phương trình tham số của đường thẳng d đi qua M, cắt và vuông góc với Δ là:
A
.
d...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm M (2 ; 1 ; 0) và đường thẳng ∆ : x - 1 2 = y + 1 1 = z - 1 . Phương trình tham số của đường thẳng d đi qua M, cắt và vuông góc với Δ là:
A . d : x = 2 + t y = 1 - 4 t z = - 2 t
B . d : x = 2 - t y = 1 + t z = t
C . d : x = 1 + t y = - 1 - 4 t z = 2 t
D . d : x = 2 + 2 t y = 1 + t z = - t
Chọn A

Gọi I = d ∩ Δ. Do I ∈ Δ nên I (2t + 1; t – 1; -t).

từ đó suy ra d có một vectơ chỉ phương là ![]() và đi qua M (2 ; 1 ; 0) nên có phương trình
và đi qua M (2 ; 1 ; 0) nên có phương trình 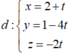
Đúng 0
Bình luận (0)
Trong mặt phẳng toạ độ Oxy, cho hai điểm A(3;1),B(4;-2) và đường thẳng d: -x+2y+1=0. a) Viết phương trình tham số của Δ đi qua A song song với đường thẳng d b) Viết phương trình tổng quát của Δ đi qua B và vuông góc với đường thẳng d c) Viết phương trình đường tròn có bán kính AB
a: (Δ)//d nên Δ: -x+2y+c=0
=>VTPT là (-1;2)
=>VTCP là (2;1)
PTTS là:
x=3+2t và y=1+t
b: (d): -x+2y+1=0
=>Δ: 2x+y+c=0
Thay x=4 và y=-2 vào Δ, ta được:
c+8-2=0
=>c=-6
Đúng 0
Bình luận (0)








