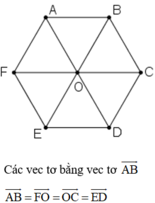
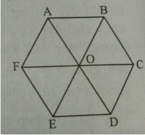
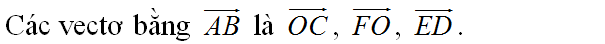Gọi O là tâm hình lục giác đều ABCDEF. Hãy chỉ ra các vectơ bằng vectơ OA→

Những câu hỏi liên quan
Cho lục giác đều ABCDEF tâm O. Hãy chỉ ra các vectơ bằng vectơ AB có điểm đầu và điểm cuối là O hoặc các đỉnh của lục giác.
Cho lục giác đều ABCDEF có tâm O.
a) Tìm các vectơ khác vectơ O→ và cùng phương với vectơ OA→.
b) Tìm các vectơ bằng vectơ AB→.
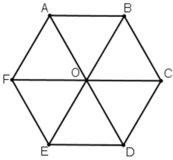
a) Các vectơ khác vectơ O→ và cùng phương với vectơ OA→ là:
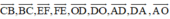
b) Các vectơ bằng vectơ AB→ là:
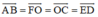
Đúng 0
Bình luận (0)
Cho hình lục giác đều ABCDEF có tâm O.
a) Tìm các vectơ bằng vectơ OA, AB
b)Ngược hướng với OC
a: \(\overrightarrow{OA}=\overrightarrow{DO}=\overrightarrow{CB}=\overrightarrow{EF}\)
\(\overrightarrow{AB}=\overrightarrow{ED}=\overrightarrow{FO}=\overrightarrow{OC}\)
Đúng 0
Bình luận (0)
Cho lục giác đều ABCDEF có tâm O. Hãy chỉ ra các vectơ bằng \(\overrightarrow{AB}\) có điểm đầu và điểm cuối là O hoặc các đỉnh của lục giác ?
Các véc tơ bằng véc tơ \(\overrightarrow{AB}\) là:
\(\overrightarrow{OC};\overrightarrow{FO};\overrightarrow{ED}\).
Đúng 0
Bình luận (0)
Gọi O là tâm hình lục giác đều ABCDEF.
a) Tìm các vectơ khác vectơ \(\overrightarrow 0 \) và cùng hướng với vectơ \(\overrightarrow {OA} \).
b) Tìm các vectơ bằng vectơ \(\overrightarrow {AB} \).
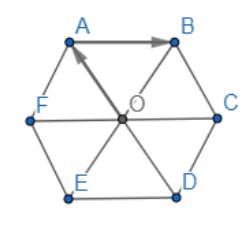
a) Ta có: AO // BC // EF
Suy ra các vectơ khác vectơ khác vectơ \(\overrightarrow 0 \) và cùng hướng với vectơ \(\overrightarrow {OA} \) là : \(\overrightarrow {DO} ,\overrightarrow {DA} ,\overrightarrow {CB} ,\overrightarrow {EF} \)
b) Ta có: \(OA = OB = OC = OD = OE = FO\) và AB // FC // ED
Suy ra các vectơ bằng vectơ \(\overrightarrow {AB} \) là \(\overrightarrow {FO} ,\overrightarrow {OC} ,\overrightarrow {ED} \)
Đúng 0
Bình luận (0)
Cho hình lục giác ABCDEF có o là tâm.hãy xác định các vectơ mà có điểm đầu và điểm cuối là đỉnh của lục giác đều và tâm o sao cho bằng vectơ AB
Chắc là lục giác đều?
Các vecto bằng \(\overrightarrow{AB}\) là \(\overrightarrow{FO};\overrightarrow{OC};\overrightarrow{ED}\)

Đúng 1
Bình luận (1)
Cho lục giác đều ABCDEF tâm O. Số các vectơ khác O A → và cùng phương với nó là
A. 5
B. 6
C. 9
D. 10
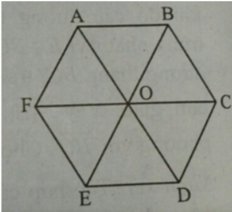
Ta có: BC // AD // EF.
Do đó, các vectơ khác O A → và cùng phương với nó là:
B C → ; C B → ; O D → ; D O → ; A O → ; A D → ; D A → ; E F → ; F E →
Vậy số các vectơ khác O A → cùng phương với nó là 9 .
Chọn C.
Đúng 0
Bình luận (0)
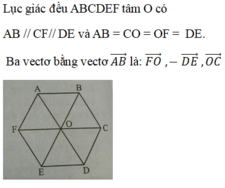
Cho lục giác đều ABCDEF tâm O. Ba vectơ bằng vectơ
A
B
→
là: A.
O
F
→
,
D
E
→
,
O
C
→
B.
F
O
→
,...
Đọc tiếp
Cho lục giác đều ABCDEF tâm O. Ba vectơ bằng vectơ A B → là:
A. O F → , D E → , O C →
B. F O → , - D E → , O C →
C. O F → , D E → , C O →
D. O F → , E D → , O C →
Cho lục giác đều ABCDEF tâm O. Số các vectơ khác vectơ
O
C
→
và có độ dài bằng nó là: A. 24 B. 11 C. 12 D. 23
Đọc tiếp
Cho lục giác đều ABCDEF tâm O. Số các vectơ khác vectơ O C → và có độ dài bằng nó là:
A. 24
B. 11
C. 12
D. 23
Do ABCDEF là lục giác đều tâm O nên AB = BC = CD= DE = EF = FA = OC.
Trên hình có tất cả 12 đoạn thẳng bằng nhau và bằng OC, tạo thành 24 vectơ có độ dài bằng OC. Trừ ra vectơ O C → còn lại 23 vectơ.
Chọn D.
Đúng 0
Bình luận (0)