Cho dãy số có giới hạn (un) xác định bởi : u 1 = 1 2 u n + 1 = 1 2 - u n , n ≥ 1 . Tìm kết quả đúng của u n .
A. 0.
B. 1.
C. -1.
D. 1 2 .
Những câu hỏi liên quan
Cho dãy số có giới hạn
(
u
n
)
xác định bởi :
u
1
1
2
u
n...
Đọc tiếp
Cho dãy số có giới hạn ( u n ) xác định bởi : u 1 = 1 2 u n + 1 = 1 2 - u n , n ≥ 1 . Tìm kết quả đúng của lim u n .
A. 0.
B. 1.
C. -1.
D. 1 2 .
Cho dãy số
(
u
n
)
xác định bởi
u
1
1
u
n
+
1...
Đọc tiếp
Cho dãy số ( u n ) xác định bởi u 1 = 1 u n + 1 = 2 u n + 3 u n + 2 v ớ i n ≥ 1
a) Chứng minh rằng u n > 0 với mọi n.
b) Biết ( u n ) có giới hạn hữu hạn. Tìm giới hạn đó.
Cho dãy số
u
n
được xác định bởi
u
1
1
,
u
n
+
1
1
2
u
n
+
2
u
n...
Đọc tiếp
Cho dãy số u n được xác định bởi u 1 = 1 , u n + 1 = 1 2 u n + 2 u n với mọi n ≥ 1 . Tìm giới hạn của u n
A. l i m u n = 1
B. l i m u n = - 1
C. l i m u n = 2
D. l i m u n = - 2
Chọn C.
Phương pháp : Dãy số giảm bị chặn dưới thì có giới hạn.
Cách giải : Dễ thấy dãy số đã cho là dãy số dương.
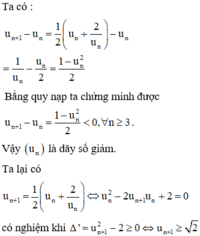
Vậy dãy số đã cho giảm và bị chặn dưới nên có giới hạn.
Đúng 0
Bình luận (0)
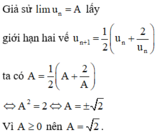
Cho dãy un xác định bởi \(u_1=1\)và \(\dfrac{u_{n-1}^2+2021}{2u_{n-1}}\).Chứng minh dãy đó có giới hạn và tìm giới hạn dãy đó
Dễ thấy \(u_n>0,\forall n\inℕ^∗\).
Ta có \(u_{n+1}-u_n=\dfrac{u_n^2+2021}{2u_n}-u_n=\dfrac{2021-u_n^2}{2u_n}\)
Với \(n\ge2\) thì \(u_n=\dfrac{u_{n-1}^2+2021}{2u_{n-1}}\) \(=\dfrac{u_{n-1}}{2}+\dfrac{2021}{2u_{n-1}}\) \(>2\sqrt{\dfrac{u_{n-1}}{2}.\dfrac{2021}{2u_{n-1}}}\) \(=\sqrt{2021}\)
Vậy \(u_n>\sqrt{2021},\forall n\ge2\), suy ra \(u_{n+1}-u_n=\dfrac{2021-u_n^2}{2u_n}< 0,\forall n\inℕ^∗\)
\(\Rightarrow\) Dãy \(\left(u_n\right)\) là dãy giảm. Mà \(u_n>\sqrt{2021}\) \(\Rightarrow\left(u_n\right)\) có giới hạn hữu hạn. Đặt \(\lim\limits_{n\rightarrow+\infty}u_n=L\) \(\Rightarrow L=\dfrac{L^2+2021}{2L}\) \(\Leftrightarrow L=\sqrt{2021}\)
Vậy \(\lim\limits_{n\rightarrow+\infty}u_n=\sqrt{2021}\)
Đúng 0
Bình luận (0)
Dễ thấy .
Ta có
Với thì
Vậy , suy ra
Dãy là dãy giảm. Mà có giới hạn hữu hạn. Đặt
Vậy
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho dãy số thực (un) xác định bởi : \(\left\{{}\begin{matrix}u_1=\dfrac{3}{2}\\u_n=\sqrt{3u_{n-1}-2},\forall n\ge2\end{matrix}\right.\)
Chứng minh dãy số (un) có giới hạn hữu hạn khi \(n\rightarrow\infty\)
Ta sẽ chứng minh dãy bị chặn trên bởi 2
Thật vậy, với \(n=1;2\) thỏa mãn
Giả sử điều đó cũng đúng với \(n=k\) , tức \(u_k< 2\)
Ta cần chứng minh \(u_{k+1}< 2\)
Ta có: \(u_{k+1}=\sqrt{3u_k-2}< \sqrt{3.2-2}=2\) (đpcm)
Tương tự, ta cũng quy nạp được dễ dàng \(u_n>1\)
Mặt khác: \(u_n-u_{n-1}=\sqrt{3u_{n-1}-2}-u_{n-1}=\dfrac{3u_{n-1}-2-u_{n-1}^2}{\sqrt{3u_{n-1}-2}+u_{n-1}}\)
\(=\dfrac{\left(2-u_{n-1}\right)\left(u_{n-1}-1\right)}{\sqrt{3u_{n-1}-2}+u_{n-1}}>0\)
\(\Rightarrow u_n>u_{n-1}\Rightarrow\) dãy tăng
Dãy tăng và bị chặn trên nên có giới hạn hữu hạn.
Gọi giới hạn đó là k thì:
\(k=\sqrt{3k-2}\Leftrightarrow k=2\)
Đúng 1
Bình luận (0)
cho dãy số un xác định bởi u1 = 2021
un+1= (un^2021 - un + 16)/(un^2020 - un + 17)
a) chứng minh un không tồn tại giới hạn hữu hạn
b) đặt Sn = Σ 1/(un^2020 + 3) tính lim Sn
Cho dãy số (Un) xác định bởi: { U1=1; Un+1=1/2un + 3/2; ∀n ϵ N*
Tình giới hạn của dãy số (Un)
Ai đó giúp em với, em cảm ơn rất nhiều ạ
29 tháng 3 2021 lúc 21:53
Cho dãy số thực (un) xác định bởi \(\left\{{}\begin{matrix}u_1=2019\\u^2_n+2018u_n-2020u_{n+1}+1=0\left(n\in N\cdot\right)\end{matrix}\right.\). Tìm giới hạn của dãy số (Sn), biết: Sn = \(\dfrac{1}{u_1+2019}+\dfrac{1}{u_2+2019}+...+\dfrac{1}{u_n+2019}\)
Đề không cho sẵn dãy tăng à? Vậy phải chứng minh nó tăng trước
\(u_{n+1}=\dfrac{u_n^2+2018u_n+1}{2020}\)
\(u_{n+1}-u_n=\dfrac{u_n^2+2018u_n+1}{2020}-u_n=\dfrac{\left(u_n-1\right)^2}{2020}\ge0\) \(\Rightarrow\) dãy tăng và không bị chặn trên \(\Rightarrow lim\left(u_n\right)=+\infty\)
\(\Rightarrow2020u_{n+1}=u_n^2+2018u_n+1\)
\(\Leftrightarrow2020u_{n+1}-2020=u_n^2+2018u_n-2019\)
\(\Leftrightarrow2020\left(u_{n+1}-1\right)=\left(u_n+2019\right)\left(u_n-1\right)\)
\(\Rightarrow\dfrac{1}{2020\left(u_{n+1}-1\right)}=\dfrac{1}{\left(u_n+2019\right)\left(u_n-1\right)}=\dfrac{1}{2020}\left(\dfrac{1}{u_n-1}-\dfrac{1}{u_n+2019}\right)\)
\(\Rightarrow\dfrac{1}{u_n+2019}=\dfrac{1}{u_n-1}-\dfrac{1}{u_{n+1}-1}\)
Thế n=1;2;...;n ta được:
\(\dfrac{1}{u_1+2019}=\dfrac{1}{u_1-1}-\dfrac{1}{u_2-1}\)
\(\dfrac{1}{u_2+2019}=\dfrac{1}{u_2-1}-\dfrac{1}{u_3-1}\)
...
\(\dfrac{1}{u_n+2019}=\dfrac{1}{u_n-1}-\dfrac{1}{u_{n+1}-1}\)
Cộng vế: \(S_n=\dfrac{1}{u_n-1}-\dfrac{1}{u_{n+1}-1}=\dfrac{1}{2018}-\dfrac{1}{u_{n+1}-1}\)
\(\Rightarrow\lim\left(S_n\right)=\dfrac{1}{2018}-\dfrac{1}{\infty}=\dfrac{1}{2018}\)
Đúng 1
Bình luận (0)
Cho dãy số (Un) được xác định như sau: \(u_1=2023\), \(u_{n-1}=n^2.\left(u_{n-1}-u_n\right)\), với mọi n thuộc N*, \(n\ge2\). Chứng minh rằng dãy số (Un) có giới hạn và tìm giới hạn đó