Cho dãy ( X k ) được xác định như sau x k = 1 2 ! + 2 3 ! + . . . + k ( k + 1 ) ! . Tìm lim u n với u n = x 1 n + x 2 n + . . . + x 2017 n n
A. + ∞
B. - ∞
C. 1 - 1 2017 !
D. 1 + 1 2017 !
Những câu hỏi liên quan
Cho dãy
(
X
k
)
được xác định như sau
x
k
1
2
!
+
2
3
!
+
.
.
.
+
k
(
k
+...
Đọc tiếp
Cho dãy ( X k ) được xác định như sau x k = 1 2 ! + 2 3 ! + . . . + k ( k + 1 ) ! Tìm với u n = x 1 n + x 2 n + . . . + x 2017 n n
A. + ∞
B. - ∞
C. 1 - 1 2017 !
D. 1 + 1 2017 !
Cho dãy
(
x
k
)
được xác định như sau:
x
k
1
2
!
+
2
3
!
+
.
.
.
+
k
(
k
+
1
)
!...
Đọc tiếp
Cho dãy ( x k ) được xác định như sau:
x k = 1 2 ! + 2 3 ! + . . . + k ( k + 1 ) !
Tìm l i m u n với u n = x 1 n + x 2 n + . . . + x 2011 n n .
30 tháng 1 2021 lúc 17:20
Cho dãy \(\left(x_k\right)\) được xác định như sau: \(x_k=\dfrac{1}{2!}+\dfrac{2}{3!}+...+\dfrac{k}{\left(k+1\right)!}\)
Tìm \(limu_n\) với \(u_n=\sqrt[n]{x_1^n+x_2^n+...+x_{2011}^n}\).
Ủa đề bài như này là sao bạn? Cho dãy x(k), nhưng lại đi tìm u(n)?
Đúng 0
Bình luận (1)
Ok start
\(\dfrac{1}{2!}=\dfrac{2!-1}{2!}=1-\dfrac{1}{2!};\dfrac{2}{3!}=\dfrac{1}{3}=\dfrac{3!-2!}{3!.2!}=\dfrac{1}{2!}-\dfrac{1}{3!}\)
\(\Rightarrow\dfrac{k}{\left(k+1\right)!}=\dfrac{1}{k!}-\dfrac{1}{\left(k+1\right)!}\)
Explain: \(\dfrac{1}{k!}-\dfrac{1}{\left(k+1\right)!}=\dfrac{\left(k+1\right)k!-k!}{k!\left(k+1\right)!}=\dfrac{k+1-1}{\left(k+1\right)!}=\dfrac{k}{\left(k+1\right)!}\)< Có nên xài quy nạp mạnh cho chặt chẽ hơn ko nhỉ?>
Nhớ lại 1 bài toán lớp 6 cũng có dạng như này
\(\Rightarrow x_k=1-\dfrac{1}{\left(k+1\right)!}\)
Xet \(x_{k+1}-x_k=1-\dfrac{1}{\left(k+2\right)!}-1+\dfrac{1}{\left(k+1\right)!}=\dfrac{1}{\left(k+1\right)!}-\dfrac{1}{\left(k+2\right)!}>0\Rightarrow x_{k+1}>x_k\)
\(\Rightarrow x_1< x_2< ...< x_{2011}\Rightarrow x_1^n< x_2^n< ...< x_{2011}^n\)
\(\Rightarrow\sqrt[n]{x_1^n+x_2^n+...+x_{2011}^n}< \sqrt[n]{x_{2011}^n+x^n_{2011}+...+x^n_{2011}}=\sqrt[n]{2011.x^n_{2011}}=x_{2011}.\sqrt[n]{2011}\)
Mat khac: \(x_{2011}=\sqrt[n]{x^n_{2011}}< \sqrt[n]{x_1^n+x_2^n+...+x_{2011}^n}\)
\(\Rightarrow x_{2011}< \sqrt[n]{x^n_1+x_2^n+...+x_{2011}^n}< \sqrt[n]{2011}x_{2011}\)
\(\lim\limits x_{2011}=1-\dfrac{1}{2012!}\)
\(\lim\limits\sqrt[n]{2011}x_{2011}=\lim\limits2011^0.x_{2011}=1-\dfrac{1}{2012!}\)
\(\Rightarrow\lim\limits\left(u_n\right)=1-\dfrac{1}{2012!}\)
Xin dung cuoc choi tai day, ban check lai xem dung ko, tinh tui hay au co khi sai :v
Đúng 0
Bình luận (0)
Cho dãy số 2 ; 6 ; 30 ;210 ; ... được xác định như sau :
Số hạng thứ k = tích k số nguyên tố đầu tiên .Biết rằng tồn tại hai số hạng của dãy số có hiệu = 30000 . Tìm 2 số hạng đó.
Gọi số nguyên tố lớn là a = 2.3.5....m; Số bé là b = 2.3.5....n (m; n là số nguyên tố)
=> a - b = 30 000
=> 2.3.5...m - 2.3.5...n = 30 000
Nhận xét nếu hai số a; b đều chứa thừa số nguyên tố là 7 thì 7 sẽ là ước của 30 000 ( Vô lí)
=> hai số a; b không có chung thừa số 7
Số lớn > 30 000 => Số bé không chứa thừa số 7 => b = 2 ; hoặc b = 2.3 = 6 hoặc b = 2.3.5 = 30
Nếu b = 2 => a = 30 002 không là số nguyên tố ( Loại)
Nếu b = 6 => a = 30 006 (Loại)
=> b = 30 => a = 30 030
Vậy 2 số đó là 6; 30 030
Đúng 0
Bình luận (0)
Nguyễn Lê Kim Uyên tớ phục bn rồi trả lời linh tinh mà vẫn được 3 l-i-k-e
Đúng 0
Bình luận (0)
Cho dãy số 2 ; 6 ; 30 ;210 ; ... được xác định như sau :
Số hạng thứ k = tích k số nguyên tố đầu tiên .Biết rằng tồn tại hai số hạng của dãy số có hiệu = 30000 . Tìm 2 số hạng đó.
Gọi số nguyên tố lớn là: a=2,3,5...m .Só bé là b=2,3,5...n(m,n là số nguyên tố)
suy ra :a-b=30000
suy ra :2,3,5...m-2,3,5...n=30000
Nhận xét nếu hai sô a,b đều chứa thừa sô nguyên tố là 7 thhif 7 sẽ là uocws của30000 (vô lí)
suy ra :hai só a,b không có chung thừa số 7
Số lớn > 30000 suy ra số bé k chứa thừa số 7 suy ra b=2,hoặc b=2.3=6 hoặc b=2,3,5=30
Nếu b=2 suy ra a=30002 không là số nguyên (loại)
Nếu b=6 suy ra a=30006(laoij)
suy ra :b=30 suy ra a=30030
Vậy 2 số đó là:6;30030
Đúng 0
Bình luận (0)
Cho dãy số tự nhiên 2, 6, 30, 210, ... được xác định như sau : số hạng thứ k bằng tích của k số nguyên tố tự nhiên ( k \(\in\)N*)
. Biết rằng tồn tại hai số hạng của dãy có hiệu là 30000 . Tìm hai số đó ?
Cho tập hợp s xác định như sau 2 e s,nếu x,ys thì 1,5:x + y es
hỏi số 9,5 có thuộc s k?
số 9,5 có thuộc tập hợp
vì sao thì mình quên rùi
Đúng 0
Bình luận (0)
Cho hình thang cong (H) giới hạn bởi các đường
y
e
x
, y 0, x -2, x 2. Đường thẳng
x
k
−
2
k
2
chia (H) thành hai phần
S
1
,
S...
Đọc tiếp
Cho hình thang cong (H) giới hạn bởi các đường y = e x , y = 0, x = -2, x= 2. Đường thẳng x = k − 2 < k < 2 chia (H) thành hai phần S 1 , S 2 như hình vẽ dưới. Cho S 1 và S 2 quay quanh trục Ox ta thu được hai khối tròn xoay có thể tích lần lượt là V 1 và V 2 . Xác định k để V 1 = V 2 .
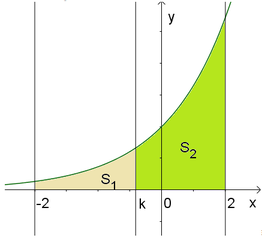
A. k = 1 2 ln e 4 − e − 4 2
B. k = 1 2 ln e 2 + e − 2 2
C. k = 1 2 ln e 4 + e − 4 2
D. k = ln e 4 + e − 4 2
Cho dãy số nguyên a gồm n phần tử được sắp xếp tăng dần. Hãy xác định giá trị lớn nhất của i sao cho ai≤x. Nếu không có vị trí thõa mãn in ra 0.InputDòng đâu tiên chứa số hai số nguyên dương n và k - độ dài của dãy, số câu hỏi. (n,k≤100000)n số, các phần tử dãy a (−109≤ai≤109)k số nguyên dương x (−109≤x≤109)OutputGồm kk dòng, mỗi dòng chứa câu trả lời cho mỗi câu hỏi.Sample Input5 5 3 3 5 8 9 2 4 8 1 10Sample Output0 2 4 0 5
Đọc tiếp
Cho dãy số nguyên a gồm n phần tử được sắp xếp tăng dần. Hãy xác định giá trị lớn nhất của i sao cho ai≤x. Nếu không có vị trí thõa mãn in ra 0.
Input
Dòng đâu tiên chứa số hai số nguyên dương n và k - độ dài của dãy, số câu hỏi. (n,k≤100000)
n số, các phần tử dãy a (−109≤ai≤109)
k số nguyên dương x (−109≤x≤109)
Output
Gồm kk dòng, mỗi dòng chứa câu trả lời cho mỗi câu hỏi.
Sample Input
5 5 3 3 5 8 9 2 4 8 1 10
Sample Output
0 2 4 0 5