Cho các số thực dương a, b với a ≠ 1 là log a b < 0 . Khẳng định nào sau đây đúng?
A. 0 < b < 1 < a 0 < a < 1 < b
B. 0 < a , b < 1 1 < a , b
C. 0 < b < 1 < a 1 < a , b
D. 0 < b , a < 1 0 < a < 1 < b
Những câu hỏi liên quan
Cho các số thực dương a, b với a≠1 và log a b 0. Khẳng định nào sau đây là đúng? A.
0
a
,
b
1
0
a
1...
Đọc tiếp
Cho các số thực dương a, b với a≠1 và log a b >0. Khẳng định nào sau đây là đúng?
A. 0 < a , b < 1 0 < a < 1 < b
B. 0 < a , b < 1 1 < a , b
C. 0 < a , b < 1 0 < b < 1 < a
D. 0 < b < 1 < a 1 < a , b
SGK Kết nối tri thức và cuộc sống
15 tháng 8 2023 lúc 19:52
Cho hai số thực dương a, b với \(a \ne 1\). Khẳng định nào sau đây là đúng?
A. \({\log _a}\left( {{a^3}{b^2}} \right) = 3 + {\log _a}b\).
B. \({\log _a}\left( {{a^3}{b^2}} \right) = 3 + 2{\log _a}b\).
C. \({\log _a}\left( {{a^3}{b^2}} \right) = \frac{3}{2} + {\log _a}b\).
D. \({\log _a}\left( {{a^3}{b^2}} \right) = \frac{1}{3} + \frac{1}{2}{\log _a}b\).
\(log_a\left(a^3b^2\right)=log_aa^3+log_ab^2=3+2\cdot log_ab\)
=>B
Đúng 0
Bình luận (0)
Cho các số thực dương a, b với
a
≠
1
là
log
a
b
0
. Khẳng định nào sau đây đúng?
Đọc tiếp
Cho các số thực dương a, b với a ≠ 1 là log a b < 0 . Khẳng định nào sau đây đúng?
Cho các số thực dương a, b với
a
≢
1
là
log
a
b
0
. Khẳng định nào sau đây đúng? A.
0
b
1
a
0
a...
Đọc tiếp
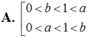
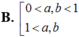
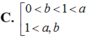
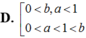
Cho các số thực dương a, b với a ≢ 1 là log a b < 0 . Khẳng định nào sau đây đúng?
A. 0 < b < 1 < a 0 < a < 1 < b
B. 0 < a , b < 1 1 < a , b
C. 0 < b < 1 < a 1 < a , b
D. 0 < b , a < 1 0 < a < 1 < b
Cho các số thực dương a,b với
a
≠
1
và
log
a
b
0
. Khẳng định nào sau đây là đúng?
Đọc tiếp
Cho các số thực dương a,b với a ≠ 1 và log a b > 0 . Khẳng định nào sau đây là đúng?
Cho các số thực dương a, b với
a
≠
1
và
log
a
b
0
.
Khẳng định nào sau đây là đúng?
Đọc tiếp
Cho các số thực dương a, b với a ≠ 1 và log a b > 0 . Khẳng định nào sau đây là đúng?
Cho các số thực dương a,b với
a
≠
1
và
log
a
b
0
. Khẳng định nào sau đây là đúng? A.
0
a
,
b
1
0
a...
Đọc tiếp
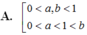
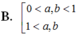
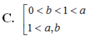
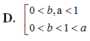
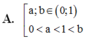
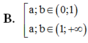
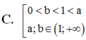
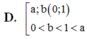
Cho các số thực dương a,b với a ≠ 1 và log a b > 0 . Khẳng định nào sau đây là đúng?
A. 0 < a , b < 1 0 < a < 1 < b .
B. 0 < a , b < 1 1 < a ,1 < b .
C. 0 < b < 1 < a 1 < a ,1 < b .
D. 0 < b , a < 1 0 < a < 1 < b .
Đáp án B
Ta có log a b > 0 ⇔ log a b > log a 1 .
Với 0 < a < 1 thì b p t ⇔ 0 < b < 1 .
Với a > 1 thì b p t ⇔ b > 1 .
Vậy ta chọn B.
Đúng 0
Bình luận (0)
Cho các số thực dương a,b với
a
≠
1
và
log
a
b
0
. Khẳng định nào sau đây là đúng? A.
0
a
,
b
1
0...
Đọc tiếp
Cho các số thực dương a,b với
a
≠
1
và
log
a
b
>
0
. Khẳng định nào sau đây là đúng?
A. 0 < a , b < 1 0 < a < 1 < b
B. 0 < a , b < 1 1 < a , b
C. 0 < b < 1 < a 1 < a , b
D. 0 < b , a < 1 0 < b < 1 < a
Đáp án là B
Ta đặt log a b = t > 0 ( a , b > 0 , a ≠ 0 )
< = > b = a t
Nếu a>1 thì b>1 (t>0)
Nếu 0<a<1 thì b = a t <1 (t>0)
Đúng 0
Bình luận (0)
Cho các số thực dương a, b với
a
≠
1
và
log
a
b
0.
Khẳng định nào sau đây là đúng? A.
a
;
b
∈
0
;
1...
Đọc tiếp
Cho các số thực dương a, b với a ≠ 1 và log a b > 0. Khẳng định nào sau đây là đúng?
A. a ; b ∈ 0 ; 1 0 < a < 1 < b
B. a ; b ∈ 0 ; 1 a ; b ∈ 1 ; + ∞
C. 0 < b < 1 < a a ; b ∈ 1 ; + ∞
D. a ; b 0 ; 1 0 < b < 1 < a
