Biết rằng phương trình z 2 + b z + c = 0 b ; c ∈ ℤ có một nghiệm phức là z 1 = 1 + 2 i . Khẳng định nào sau đây đúng?
A. b + c = 0
B. b + c = 2
C. b + c = 3
D. b + c = 7
Tìm hai số thực b và c biết rằng phương trình z 2 + b z + c = 0 có nghiệm phức z = 1+i
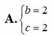
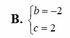
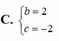
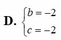
Tìm hai số thực b và c biết rằng phương trình z 2 + b z + c = 0 có nghiệm phức z=1+i.
A. b = 2 c = 2
B. b = - 2 c = 2
C. b = 2 c = - 2
D. b = - 2 c = - 2
Biết rằng phương trình z 2 + bz + c = 0 (b,c∈R) có một nghiệm phức là z=1+2i. Khẳng định nào sau đây là đúng?
A. b+c= 0.
B. b+c= 2.
C. b+c= 3.
D. b+c=7.
Cho phương trình z 3 + a z 2 + b z + c = 0 Nếu z=1-i và z=1 là 2 nghiệm của phương trình thì a - b - c bằng
A. 2
B. 3
C. 5
D. 6
Cho phương trình z 3 + a z 2 + b z + c = 0 nhận z = 2 và z = 1 + i làm các nghiệm của phương trình. Khi đó a - b + c là
![]()
![]()
![]()
![]()
Tìm các số thực a,b,c để phương trình (ẩn z) z 3 + a z 2 + b z + c = 0 nhận z = 1 + i và z = 2 làm nghiệm
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho bốn điểm A(0;0;1), B(1;2;4), C(1;0;1) và D(2;1;2). Gọi (P) là mặt phẳng qua C,D và song song với đường thẳng AB. Phương trình của (P) là:
A. x - 2y + z - 2 = 0.
B. 3x - 2y - z - 2 = 0.
C. 3x - z - 2 = 0.
D. 3x - 2y - z - 1 = 0.
\(\overrightarrow{AB}=\left(1;2;3\right)\) ; \(\overrightarrow{CD}=\left(1;1;1\right)\)
\(\left[\overrightarrow{AB};\overrightarrow{CD}\right]=\left(-1;2;-1\right)=-\left(1;-2;1\right)\)
Phương trình (P):
\(1\left(x-1\right)-2y+1\left(z-1\right)=0\Leftrightarrow x-2y+z-2=0\)
Để tìm phương trình mặt phẳng (P) ta cần tìm được vector pháp tuyến của mặt phẳng. Vì mặt phẳng (P) song song với đường thẳng AB nên vector pháp tuyến của (P) cũng vuông góc với vector chỉ phương của AB, tức là AB(1-0;2-0;4-1)=(1;2;3).
Vì (P) đi qua C(1;0;1) nên ta dễ dàng tìm được phương trình của (P) bằng cách sử dụng công thức phương trình mặt phẳng:
3x - 2y - z + d = 0, trong đó d là vế tự do.
Để tìm d, ta chỉ cần thay vào phương trình trên cặp tọa độ (x;y;z) của điểm C(1;0;1):
3(1) -2(0) - (1) + d = 0
⇒ d = -2
Vậy phương trình của mặt phẳng (P) là:
3x - 2y - z - 2 = 0,
và đáp án là B.
→AB=(1;2;3)��→=(1;2;3) ; −−→CD=(1;1;1)��→=(1;1;1)
[−−→AB;−−→CD]=(−1;2;−1)=−(1;−2;1)[��→;��→]=(−1;2;−1)=−(1;−2;1)
Phương trình (P):
1(x−1)−2y+1(z−1)=0⇔x−2y+z−2=0
Biết phương trình z 2 + a z + b = 0 có một nghiệm là z = - 2 + i Tính a+b
A. 9
B. 1
C. 4
D. -1
Cho phương trình z 3 + a z 2 + b z + c = 0 . Nếu z = 1 − i và z = 1 là hai nghiệm của phương trình thì a − b − c bằng (a, b, c là số thực).
A. 2
B. 3
C. 5
D. 6
Biết phương trình z 2 + a z + b = 0 ( a , b ∈ ℝ ) có một nghiệm là: z=-2+i. Tính a-b.
A. 9
B. 1
C. 4
D. -1
Đáp án D
Thay z=-2+i vào phương trình ta được:
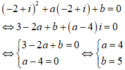
Vậy a-b=4-5=-1
Cách khác. Nghiệm liên hợp của nghiệm z 1 = - 2 + i là z 2 = - 2 - i
Ta có ![]() nên
z
1
,
z
2
là nghiệm của phương trình
nên
z
1
,
z
2
là nghiệm của phương trình ![]()
Do đó suy ra ![]()