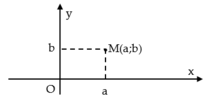
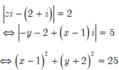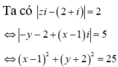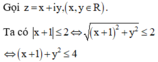Trên mặt phẳng Oxy, tìm tập hợp các điểm M biểu diễn số phức z thỏa mãn điều kiện 1 ≤ z - 2 i < 2
A. Hình tròn tâm I ( 0;2 ) và bán kính R = 2
B. Hình tròn tâm I ( 0;2 )và bán kính R = 1
C. Hình tròn tâm I ( 0;2 ) và bán kính R = 1 đồng thời trừ đi phần trong của hình tròn tâm I ( 0;2 ) bán kính R' = 1
D. Hình tròn tâm I ( 0;2 ) và bán kính R = 1 đồng thời trừ đi hình tròn tâm I ( 0;2 ) bán kính R' = 1