với các số dương a+b+c giả sử 1/a +1/b+1/c >a+b+c
cmr a+b+c>3abc
Những câu hỏi liên quan
nếu a,b,c là các số dương thoẳ mãn 1/a + 1/b +1/c >= a+b+c thì a+b + c >= 3abc
Ta có:
\(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge a+b+c\)
<=>\(\frac{ab+bc+ca}{abc}\ge a+b+c\)
Mà \(ab+bc+ca\le\frac{\left(a+b+c\right)^2}{3}\)
Suy ra \(\frac{\left(a+b+c\right)^2}{3}.\frac{1}{abc}\ge a+b+c\)
Hay \(a+b+c\ge3abc\)(đpcm)
Dấu "=" xảy ra <=>a=b=c
Giả sử a , b , c là các số thực dương sao cho a+b+c=1
Chứng minh rằng : \(2\left(\frac{b}{a}+\frac{c}{b}+\frac{a}{c}\right)\ge\frac{1+a}{1-a}+\frac{1+b}{1-b}+\frac{1+c}{1-c}\)
\(2\left(\frac{b}{a}+\frac{c}{b}+\frac{a}{c}\right)\ge\frac{1+a}{1-a}+\frac{1+b}{1-b}+\frac{1+c}{1-c}\)
Thay thế \(a+b+c=1\)
\(\Leftrightarrow2\left(\frac{b}{a}+\frac{c}{b}+\frac{a}{c}\right)\ge\frac{2a+b+c}{b+c}+\frac{a+2b+c}{a+c}+\frac{a+b+2c}{a+b}\)
\(\Leftrightarrow2\left(\frac{b}{a}+\frac{c}{b}+\frac{a}{c}\right)\ge\frac{2a}{b+c}+\frac{2b}{a+c}+\frac{2c}{a+b}+3\)
\(\Leftrightarrow\frac{2b}{a}+\frac{2c}{b}+\frac{2a}{c}\ge\frac{2a}{b+c}+\frac{2b}{a+c}+\frac{2c}{a+b}+3\)
\(\Leftrightarrow\left(\frac{2b}{a}-\frac{2b}{a+c}\right)+\left(\frac{2c}{b}-\frac{2c}{a+b}\right)+\left(\frac{2a}{c}-\frac{2a}{b+c}\right)\ge3\)
\(\Leftrightarrow\frac{2bc}{a\left(a+c\right)}+\frac{2ca}{b\left(a+b\right)}+\frac{2ab}{c\left(b+c\right)}\ge3\)
\(\Leftrightarrow\frac{bc}{a\left(a+c\right)}+\frac{ca}{b\left(a+b\right)}+\frac{ab}{c\left(b+c\right)}\ge\frac{3}{2}\)
\(\Leftrightarrow\frac{\left(bc\right)^2}{abc\left(a+c\right)}+\frac{\left(ca\right)^2}{abc\left(a+b\right)}+\frac{\left(ab\right)^2}{abc\left(b+c\right)}\ge\frac{3}{2}\)
Áp dụng bất đẳng thức cộng mẫu số
\(\Rightarrow\frac{\left(bc\right)^2}{abc\left(a+c\right)}+\frac{\left(ca\right)^2}{abc\left(a+b\right)}+\frac{\left(ab\right)^2}{abc\left(b+c\right)}\)
\(\ge\frac{\left(ab+bc+ca\right)^2}{abc\left(a+b+c+a+b+c\right)}=\frac{\left(ab+bc+ca\right)^2}{2abc}\)
Chứng minh rằng : \(\frac{\left(ab+bc+ca\right)^2}{2abc}\ge\frac{3}{2}\)
\(\Leftrightarrow2\left(ab+bc+ca\right)^2\ge6abc\)
\(\Leftrightarrow\left(ab+bc+ca\right)^2\ge3abc\)
\(\Leftrightarrow a^2b^2+b^2c^2+c^2a^2+2ab^2c+2abc^2+2a^2bc\ge3abc\)
\(\Leftrightarrow a^2b^2+b^2c^2+c^2a^2+2abc\left(a+b+c\right)\ge3abc\)
\(\Leftrightarrow a^2b^2+b^2c^2+c^2a^2+2abc\ge3abc\)
\(\Leftrightarrow a^2b^2+b^2c^2+c^2a^2\ge abc\)
Áp dụng bất đẳng thức Cauchy cho 2 bộ số thực không âm
\(\Rightarrow\hept{\begin{cases}a^2b^2+b^2c^2\ge2\sqrt{a^2b^4c^2}=2ab^2c\\b^2c^2+c^2a^2\ge2\sqrt{a^2b^2c^4}=2abc^2\\a^2b^2+c^2a^2\ge2\sqrt{a^2b^2c^2}=2a^2bc\end{cases}}\)
\(\Leftrightarrow2\left(a^2b^2+b^2c^2+c^2a^2\right)\ge2abc\left(a+b+c\right)\)
\(\Leftrightarrow a^2b^2+b^2c^2+c^2a^2\ge abc\left(đpcm\right)\)
Vì \(\frac{\left(ab+bc+ca\right)^2}{2abc}\ge\frac{3}{2}\)
Vậy \(\frac{\left(bc\right)^2}{abc\left(a+c\right)}+\frac{\left(ca\right)^2}{abc\left(a+b\right)}+\frac{\left(ab\right)^2}{abc\left(b+c\right)}\ge\frac{3}{2}\)
\(\Leftrightarrow2\left(\frac{b}{a}+\frac{c}{b}+\frac{a}{c}\right)\ge\frac{1+a}{1-a}+\frac{1+b}{1-b}+\frac{1+c}{1-c}\left(đpcm\right)\)
Chúc bạn học tốt !!!
Giả sử a,b,c\(\ge\)1.Tìm GTLN của bt T=a+b+c+ab+bc+ca-3abc
Đặt a = x + 1, b = y + 1, c = z + 1. Ta có \(x,y,z\ge0\)
Khi đó ta có :
\(T=x+1+y+1+z+1+\left(x+1\right)\left(y+1\right)+\left(y+1\right)\left(z+1\right)+\left(z+1\right)\left(x+1\right)-3\left(x+1\right)\left(y+1\right)\left(z+1\right)\)
\(T=3-2\left(xy+yz+zx\right)-3xzy\le3\)
Dâu bằng xảy ra khi 2 trong ba số x, y, z bằng 0.
Vậy GTLN của T là 3 khi 2 trong ba số a, b, c là 1.
Đúng 0
Bình luận (0)
Giả sử a,b,c là các số thực dương thỏa mãn \(a\le b\le3\le c,c\ge b+1,a+b\ge c\)tìm GTNN của
\(M=\frac{2ab+a+b+c\left(ab-1\right)}{\left(a+1\right)\left(b+1\right)\left(c+1\right)}\)
cho a,b,c là các số thực dương. chứng minh rằng a^2b/ab^2+1 + b^2c/bc^2+1 + c^2a/ca^2+1 >= 3abc/1+abc
VT=\(\frac{a^2}{ab+\frac{1}{b}}+\frac{b^2}{bc+\frac{1}{c}}+\frac{c^2}{ca+\frac{1}{a}}\)
áp dụng bđt cộng mẫu đc VT \(\ge\frac{\left(a+b+c\right)^2}{ab+bc+ca+\frac{1}{a}+\frac{1}{b}+\frac{1}{c}}=\frac{\left(a+b+c\right)^2}{ab+bc+ca+\frac{ab+bc+ca}{abc}}\left(1\right)\)
Ta có \(ab+bc+ca\le\frac{\left(a+b+c\right)^2}{3}\forall a,b,c\)
Nên \(\left(1\right)\ge\frac{\left(a+b+c\right)^2}{\frac{\left(a+b+c\right)^2}{3}+\frac{\left(a+b+c\right)^2}{3abc}}=\frac{1}{\frac{1}{3}+\frac{1}{3abc}}=\frac{3abc}{1+abc}\left(đccm\right)\)
dấu bằng xảy ra <> a=b=c
Cho a,b,c dương , a+b+c= 1/a + 1/b + 1/c
CMR a+b+c >= 3abc
Ta có:
\(a+b+c=\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\)
\(\Leftrightarrow\frac{a+b+c}{ab+bc+ca}=\frac{1}{abc}\)
Ta lại có:
\(\frac{a+b+c}{ab+bc+ca}\ge\frac{3\left(a+b+c\right)}{\left(a+b+c\right)^2}=\frac{3}{a+b+c}\)
Từ đó ta có:
\(\frac{1}{abc}\ge\frac{3}{a+b+c}\)
\(\Leftrightarrow a+b+c\ge3abc\left(DPCM\right)\)
Đúng 0
Bình luận (0)
\(\Leftrightarrow\)a+b+c\(\ge\)3abc(DPCM)
Đúng 0
Bình luận (0)
\(\Leftrightarrow\)a+b+c\(\ge\)3abc(DPCM)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giả sử
1
+
2
i
1
-
i
là một nghiệm ( phức ) của phương trình
a
x
2
+
b
x
+
c
0
trong đó a, b, c là các số nguyên dương. Thế thì
a
+
b
+
c
nhỏ nhất bằng A. 8 ...
Đọc tiếp
Giả sử 1 + 2 i 1 - i là một nghiệm ( phức ) của phương trình a x 2 + b x + c = 0 trong đó a, b, c là các số nguyên dương. Thế thì a + b + c nhỏ nhất bằng
A. 8
B. 9
C. 10
D. 11
Chọn B.
Đặt
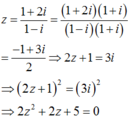
Điều này chứng tỏ z là một nghiệm (phức) của phương trình 2 x 2 + 2 x + 5 = 0
Từ đó suy ra
Đúng 0
Bình luận (0)
giả sử a;b;c là các số có a+b+c=259 và (1/a+b)+(1/b+c)+1/a+c
tính (a/b+c)+(b/a+c)+c/a+b
giả sử a,b,c là các số thực dương CMR
\(\dfrac{b^2c^3}{a^2\left(b+c\right)^3}+\dfrac{c^2a^3}{b^2\left(a+c\right)^3}+\dfrac{a^2c^3}{c^2\left(a+b\right)^3}\ge\dfrac{9abc}{4\left(3abc+ab^2+bc^2+ca^2\right)}\)