A. − − 9 + − 1 = 10
B. − 1 + 1 = 2
C. 2 + − 3 = − 1
D. 4 + − 4 = 0
A =9^9+1/9^10+1
B=10^9+1/10^10+1
so sanh a va b
A = 387420490 ; B = 1000000001
vậy B lớn hơn A
So sánh
a, A= 10^11-1/10^12-1 và B = 10^10+1/10^11+1
b, A= -9/10^2010+-19/10^2011 và B = -9/10^2011+-19/10^2010
cho A=1/1*2+1/3*4+...+1/9*10 va B=1/6*10+1/7*9+1/8*8+1/9*7+1/10*6 tinh A/B
So sánh
a,A=\(x = {{7^{10}+1} \over {7^{10}-1}}\) và B= \(x = {{7^{10}-1} \over {7^{10}-3}}\)
b,A=\({9^{10}+1} \over {9^{10}-1}\) và B=\({9^{10}+1} \over {9^{10}-3}\)
bị ngáo lol ak
[1] Cho hai tập hợp A = { 1; 5; 9; 13 ;17; 21; 25 } và B = { 0; 1; 3; 5; 10 ; 13 }. Tìm A \(\cap B\)
A. A ∩ B = { 0; 1; 3; 5; 9; 10; 13; 17; 21; 25 } B. A ∩ B = { 1; 5; 13 }
C. A ∩ B = { 9; 17; 21; 25 } D. A ∩ B = { 0; 3; 10}
Ta có:
Tập hợp A:
\(A=\left\{1;5;9;13;17;21;25\right\}\)
Tập hợp B:
\(B=\left\{0;1;3;5;10;13\right\}\)
Mà: \(A\cap B\)
\(\Rightarrow A\cap B=\left\{1;5;13\right\}\)
⇒ Chọn B
a) Cho A = \(\frac{9^{18}+1}{9^{19}+1}\)và B = \(\frac{9^{19}+1}{9^{20}+1}\). So sánh A và B
b) Cho A = \(\frac{10^{2017}-1}{10^{2018}-1}\)và B = \(\frac{10^{2018}-1}{10^{2019}-1}\). So sánh A và B
a) Ta có : B = \(\frac{9^{19}+1}{9^{20}+1}\)< \(\frac{9^{19}+1+8}{9^{20}+1+8}\)= \(\frac{9^{19}+9}{9^{20}+9}\)= \(\frac{9\left(9^{18}+1\right)}{9\left(9^{19}+1\right)}\)= \(\frac{9^{18}+1}{9^{19}+1}\)= A
Vậy A > B
b) Ta có : B = \(\frac{10^{2018}-1}{10^{2019}-1}\)> \(\frac{10^{2018}-1-9}{10^{2019}-1-9}\)= \(\frac{10^{2018}-10}{10^{2019}-10}\)= \(\frac{10\left(10^{2017}-1\right)}{10\left(10^{2018}-1\right)}\)= \(\frac{10^{2017}-1}{10^{2018}-1}\)= A
Vậy A < B.
NHỚ K CHO MK VỚI NHÉ !!!!!!!!
a)
\(9A=\frac{9^{19}+9}{9^{19}+1}=\frac{9^{19}+1+8}{9^{19}+1}=1+\frac{8}{9^{19}+1}\)
\(9A=\frac{9^{20}+9}{9^{20}+1}=\frac{9^{20}+1+8}{9^{20}+1}=1+\frac{8}{9^{20}+1}\)
ta thấy \(9^{19}+1< 9^{20}+1\Rightarrow\frac{8}{9^{19}+1}>\frac{8}{9^{20}+1}\)
\(\Rightarrow9A>9B\Rightarrow A>B\)
A= 108 + 1 /109 + 1 và B = 109 + 1/ 1010 + 1 Hãy so sánh A và B
\(taco\)
\(A=\frac{10^8+1}{10^9+1}\Rightarrow10A=1+\frac{9}{10^9+1}\)
\(B=\frac{10^9+1}{10^{10}+1}\Rightarrow10B=1+\frac{9}{10^{10}+1}\)
\(Vì:\frac{9}{10^9+1}>\frac{9}{10^{10}+1}\Rightarrow10A>10B\Rightarrow A>B\)
Ta có:
\(A=\frac{10^8+1}{10^9+1}\Leftrightarrow10A=\frac{10^9+10}{10^9+1}=\frac{10^9+1+9}{10^9+1}=1+\frac{9}{10^9+1}\)
\(B=\frac{10^9+1}{10^{10}+1}\Leftrightarrow10B=\frac{10^{10}+10}{10^{10}+1}=\frac{10^{10}+1+9}{10^{10}+1}=1+\frac{9}{10^{10}+1}\)
Vì \(\frac{9}{10^9+1}>\frac{9}{10^{10}+1}\)nên \(1+\frac{9}{10^9+1}>1+\frac{9}{10^{10}+1}\)
\(\Rightarrow10A>10B\)\(\Rightarrow A>B\)
Vậy A>B
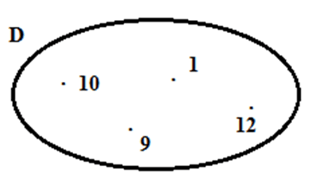
Tập hợp D là?
A. D = {8; 9; 10; 12}
B. D = {1; 9; 10}
C. D = {9; 10; 12}
D. D = {1; 9; 10; 12}
Tập hợp D là?
A. D = {8; 9; 10; 12}
B. D = {1; 9; 10}
C. D = {9; 10; 12}
D. D = {1; 9; 10; 12}
So sánh:
a, A= \(\frac{10^8+2}{10^8-1}\) ; B= \(\frac{10^8}{10^8-3}\)
b, A= \(\frac{8^{10}+1}{8^{10}-1}\) ; B=\(\frac{8^{10}-1}{8^{10}-3}\)
c, A= \(\frac{100^9+4}{100^9-1}\): B= \(\frac{100^9+1}{100^9-4}\)
mk giải cho câu A rồi tự suy mấy câu khác nhé!
ta có : A = 10^8 + 2/10^8 - 1
=> A = 10^8 - 1 + 3/10^8 - 1
=> A = 1+ 3/10^8 - 1
B = 10^8/10^8 - 3
=> B = 10^8 - 3 + 3/10^8 - 3
=> B = 1+ 3/10^8 - 3
vì 3/10^8 - 1 < 3/10^8 - 3
=> 1 + 3/10^8 - 1 < 1 + 3/10^8 - 3
=> A < B
vậy A < B
cách này cô dạy mk đó