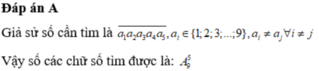Gọi các số thỏa ycbt là \(\overline{abcd}\).

 Xét trường hợp \(a\le3\). Do \(d\) là số lẻ nên \(d\in\left\{1;3;5;7\right\}\) (4 cách)

 Với mỗi cách chọn d, a có 6 cách chọn, b có 6 cách chọn và c có 5 cách chọn. Suy ra có \(4.6.6.5=720\) số

 Xét trường hợp \(a=4\). Nếu \(b=0\) thì c có 6 cách chọn. Nếu c lẻ (4 cách chọn) thì d có 3 cách chọn \(\Rightarrow\) Có \(4.3=12\) số. Nếu c chẵn (2 cách chọn) thì d có 4 cách chọn \(\Rightarrow\) Có \(2.4=8\) số. Do đó, có tất cả \(12+8=20\) số dạng \(\overline{40cd}\) thỏa ycbt.

 Nếu \(b=1\) thì c có 4 cách chọn. Nếu \(c=3\) thì \(d\in\left\{5;7\right\}\) (có 2 số). Nếu c chẵn (3 cách) thì d có 3 cách. \(\Rightarrow\) Có \(3.3=9\) số. Vậy có tất cả \(2+9=11\) số dạng \(\overline{41cd}\) thỏa ycbt.

 Vậy có \(20+11=31\) số dạng \(\overline{4bcd}\) thỏa ycbt. Do đó, có tất cả \(720+31=751\) số thỏa ycbt.

1. số tự nhiên có dạng abce ( nhớ gạch trê đầu ( vì đây là số tự nhiên))

*  ta có h là :

        h= mn 

           trong đó tập hợp mn là {0,1}

               => có 2 trường hợp xảy ra 

                (m,n)=(1,0) hoặc (0,1)

*  ta có số tự nhiên abhe có tập hợp {h,2,3,4,5,6,7,8,9}

    a có 9 cách chọn 

b có 8 cách chọn 

c có 7 cách chọn 

e có 6 cách chọn 

vậy có 9*8*7*6=3024 số

 *ta  phải loại trường hợp h  đứng đầu và có dạng 01

 trường hợp h  đứng đầu và có dạng 01 có số cách chọn là :

a có 1 cách chọn  là h

b có 8 cách 

c có 7 cách 

e có 6 cách 

=>  có 1*8*7*6=336 số 

 vậy số tự nhiên theo yêu cầu đề bài có tổng cộng

3024 - 332688 số 

0 chắc

Đáp án A

Giả sử số cần tìm là

Vậy số các chữ số tìm được là: A 9 5

Đáp án C

Phương pháp:

-Sử dụng kiến thức về chỉnh hợp

Cách làm: 

5 chữ số trong số tự nhiên có 5 chữ số cần tìm được lấy ra từ tập hợp gồm 9 phần tử 

A = 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9

Mỗi số tự nhiên có 5 chữ số cần tìm là một chỉnh hợp chập 5 của 9 phần tử trong tập hợp A.

Nên có  A 9 5  số tự nhiên có 5 chữ số cần tìm.

Đáp án C

Phương pháp: 

-Sử dụng kiến thức về chỉnh hợp 

Cách làm:  

5 chữ số trong số tự nhiên có 5 chữ số cần tìm được lấy ra từ tập hợp gồm 9 phần tử

Mỗi số tự nhiên có 5 chữ số cần tìm là một chỉnh hợp chập 5 của 9 phần tử trong tập hợp A.

Nên có số tự nhiên có 5 chữ số cần tìm

Đáp án A

Giả sử số cần tìm là  a 1 a 2 a 3 a 4 a 5 ¯ , a i ∈ { 1 ; 2 ; 3 ; ... ; 9 } , a i ≠ a j ∀ i ≠ j

Vậy số các chữ số tìm được là:  A 9 5