nghiệm nhỏ nhất của phương trình : x3-6x2-25x-18 =0

Những câu hỏi liên quan
Cho phương trình
y
x
3
-
6
x
2
+
9
x
-
2
và các phát biểu sau:(1) x 0 là nghiệm duy nhất của phương trình(2) Phương trình có nghiệm dương (3) Cả 2 nghiệm của phương trình đều nhỏ hơn 1(4) Phương trình trên có tổng 2 nghiệm là:
-
log...
Đọc tiếp
Cho phương trình y = x 3 - 6 x 2 + 9 x - 2 và các phát biểu sau:
(1) x = 0 là nghiệm duy nhất của phương trình
(2) Phương trình có nghiệm dương
(3) Cả 2 nghiệm của phương trình đều nhỏ hơn 1
(4) Phương trình trên có tổng 2 nghiệm là: - log 5 3 7
Số phát biểu đúng là:
A. 1
B. 2
C. 3
D. 4
Nghiệm nhỏ nhất của phương trình x3-6x2-25x-18=0 là x=?
\(x^3-6x^2-25x-18=0\)
<=> \(x^3-9x^2+3x^2-27x+2x-18=0\)
<=> \(x^2\left(x-9\right)+3x\left(x-9\right)+2\left(x-9\right)=0\)
<=> \(\left(x-9\right)\left(x^2+3x+2\right)=0\)
<=> \(\left(x-9\right)\left(x+1\right)\left(x+2\right)=0\)
..................
làm nốt
Đúng 0
Bình luận (0)
Nghiệm nhỏ nhất của phương trình
x3-6x2-25x-18=0 là x bằng bao nhiêu?
\(x^3-6x^2-25x-18=0\)
\(\Leftrightarrow x^2\left(x+1\right)-7x\left(x+1\right)-18\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2-7x-18\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+2x-9x-18\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left[x\left(x+2\right)-9\left(x+2\right)\right]=0\)
\(\Leftrightarrow\left(x+1\right)\left(x+2\right)\left(x-9\right)=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x+1=0\\x+2=0\\x-9=0\end{array}\right.\Leftrightarrow\left[\begin{array}{nghiempt}x=-1\\x=-2\\x=9\end{array}\right.\)
Vậy nghiệm nhỏ nhất của phương trình là \(-2\)
Đúng 0
Bình luận (0)
Nghiệm nhỏ nhất của phương trình x3 - 6x2 - 25x - 18 = 0
(ghi cach giai rõ ràng dùm mình)
Ta có:x^3-6x^2-25x-18=0 <=> x^3+2x^2-8x^2-16x-9x-18=0
<=> x^2 (x+2)-8x(x+2)-9(x+2)=0 <=> (x+2)(x2+x−9x−9)=0⇔(x+2)(x+1)(x−9)=0
Vậy x=-2;-1;9 hay x min = -2
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hàm số
y
-
x
3
+
6
x
2
-
9
x
+
4
là bảng biến thiên như hình bên dướiCác giá trị của tham số m sao cho phương trình
-
x
3
+
6
x
2
-
9
x
-
m
0
có ba nghiệm phân biệt là A. -3 m 1 B. 0 m 4 C. -4 m 0 D. 1 m...
Đọc tiếp
Cho hàm số y = - x 3 + 6 x 2 - 9 x + 4 là bảng biến thiên như hình bên dưới
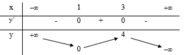
Các giá trị của tham số m sao cho phương trình - x 3 + 6 x 2 - 9 x - m = 0 có ba nghiệm phân biệt là
A. -3 < m < 1
B. 0 < m < 4
C. -4 < m < 0
D. 1 < m < 3
Cho hàm số
f
x
x
3
-
6
x
2
+
9
x
. Đặt
f
k
x
f
f
k
-
1
x
với k là số tự nhiên lớn hơn 1. Tính số ng...
Đọc tiếp
Cho hàm số f x = x 3 - 6 x 2 + 9 x . Đặt f k x = f f k - 1 x với k là số tự nhiên lớn hơn 1. Tính số nghiệm của phương trình f 6 x = 0 .
A. 729
B. 365
C. 730
D. 364
Cho hàm số
f
x
x
3
−
6
x
2
+
9
x
.
Đặt
f
k
x
f
f
k
−
1
x
(với k là số tự nhiên lớn hơn 1)....
Đọc tiếp
Cho hàm số f x = x 3 − 6 x 2 + 9 x . Đặt f k x = f f k − 1 x (với k là số tự nhiên lớn hơn 1). Tính số nghiệm của phương trình f 6 x = 0
A. 729
B. 365
C. 730
D. 364
Đáp án B
Ta có f x = x x − 3 2 ; f x = 0 ⇔ x = 0 x = 3 .
Gọi a k là số nghiệm của phương trình f k x = 0 và b k là số nghiệm của phương trình f k x = 3.
Khi đó a k = a k − 1 + b k − 1 b k = 3 k k ∈ ℕ * , k ≥ 2
suy ra a n = a n − 1 + 3 n − 1 → a n = a 1 + 3 n − 3 2 * .
Mà a 1 = 2 nên suy ra * ⇔ a n = 2 + 3 n − 3 2 = 3 n + 1 2 .
Với n = 6 ⇒ f 6 x = 0 có 3 6 + 1 2 = 365 nghiệm.
Đúng 0
Bình luận (0)
Cho (x; y; z) là nghiệm của hệ phương trình
36
x
2
y
−
60
x
2
+
25
y
0
36...
Đọc tiếp
Cho (x; y; z) là nghiệm của hệ phương trình 36 x 2 y − 60 x 2 + 25 y = 0 36 y 2 z − 60 y 2 + 25 z = 0 36 z 2 x − 60 z 2 + 25 x = 0 . Giá trị nhỏ nhất của A = x + y + z là:
A. A = 0
B. A = 5 2
C. A = 1
D. A = −2
36 x 2 y − 60 x 2 + 25 y = 0 36 y 2 z − 60 y 2 + 25 z = 0 36 z 2 x − 60 z 2 + 25 x = 0 ⇔ y = 60 x 2 36 x 2 + 25 z = 60 y 2 36 y 2 + 25 x = 60 z 2 36 z 2 + 25 ⇒ x , y , z ≥ 0
Nhận thấy x = y = z = 0 là một nghiệm của hệ phương trình
Xét x > 0; y > 0; z > 0 áp dụng bất đẳng thức Cosi cho hai số không âm ta có:
36 x 2 + 25 ≥ 2 36 x 2 .25 = 60 | x | ≥ 60 x ⇒ y ≤ x
Chứng minh tương tự, ta được z ≤ y ; x ≤ z ⇒ x ≤ z ≤ y ≤ x ⇒ x = y = z
Thay vào phương trình (1) ta được 36 x 3 – 60 x 2 + 25 x = 0 ⇔ x = 5 6
hay x = y = z = 5 6
Suy ra giá trị nhỏ nhất của A = x + y + z = 0 (khi x = y = z = 0)
Đáp án:A
Đúng 0
Bình luận (0)
Cho đồ thị hàm số
y
x
3
-
6
x
2
+
9
x
-
2
như hình vẽKhi đó phương trình
|
x
3
-
6
x
2
+
9
x
-
2
|
m
(m là tham số ) có 6 nghiệm phân biệt k...
Đọc tiếp
Cho đồ thị hàm số y = x 3 - 6 x 2 + 9 x - 2 như hình vẽ
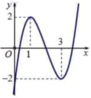
Khi đó phương trình | x 3 - 6 x 2 + 9 x - 2 | = m (m là tham số ) có 6 nghiệm phân biệt khi và chỉ khi
A. -2≤m≤2
B. 0<m<2
C. 0≤m≤2
D. -2<m<2
Chọn B
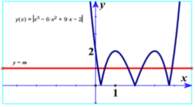
+ Đồ thị hàm số y = | x 3 - 6 x 2 + 9 x - 2 | có được bằng cách biến đổi đồ thị (C) hàm số y = x 3 - 6 x 2 + 9 x - 2
Giữ nguyên phần đồ thị (C) nằm trên trục hoành.
Lấy đồi xứng phần đồ thị của (C) phần dưới trục hoành qua trục hoành.
Xóa phần đồ thị còn lại (C) phía dưới trục hoành.
+ Số nghiệm của phương trình | x 3 - 6 x 2 + 9 x - 2 | = m là số giao điểm của đồ thị hàm số
y = | x 3 - 6 x 2 + 9 x - 2 | và đồ thị hàm số y=m. Để phương trình có 6 nghiệm phân biệt thì điều kiện cần và đủ là 0<m<2.
Đúng 0
Bình luận (0)













